Мы увидели, как при отсутствии следов движения этого автомобиля наши «виртуальные эксперты», используя различные предположения, а то и прямо манипулируя физическими законами, вместо фактической скорости Ауди в момент столкновения 60 км/ч могут насчитать этому автомобилю от 85 до 106 км/ч.
Перефразируя Тютчева, можно сказать, что умом наших экспертов не понять, аршином общим (в смысле общепринятого образования в области естественных наук) не измерить: у них особенная стать – экспертам можно только верить (или не верить).
Ну, для нашего виртуального ДТП вы обоснованно (ответ-то знаете) не поверите скорости 95 км/ч, а дальше, господа адвокаты, что? Повторка? Так они этого и ждут. И «учтя все» в пользу водителя Ауди, принесут вам уже 85 км/ч, и скажут, что меньше уже некуда, а их предположения – так они в пользу водителя, прямая из места столкновения в конечное положение – это ведь кратчайшее расстояние.
Можно возражать, что дело не столько в прямой-кривой, сколько в сочетании длин пути заноса и пути качения, но … Суд им будет верить, как и предрек поэт.
Возражать же оппонентам надо по-другому. Так как следов, однозначно свидетельствующих о неуправляемом движении хотя бы одного автомобиля в конечное положение нет, надо исследовать весть возможный диапазон – в расчетах по закону сохранения количества движения либо надо принимать возможный диапазон количества движения, от наименьшего до наибольшего, либо воспользоваться другими законами физики и методами.
В самом деле, во втором расчете в ч.1 статьи, где получалась скорость Ауди 85 км/ч, убираем в формуле для расчета скорости Ауди после удара расстояние до конечного положения 15.2 м, вместо этого числа ставим 0 – нам неизвестно расстояние, которое прошел бы Ауди, будучи заторможенным.

Этому решению можно верить – скорость Ауди в момент столкновения была не менее 43 км/ч. Это единственное, что можно определенно получить из закона сохранения количества движения для данного случая.
В механике известно четыре закона сохранения: массы, энергии, количества движения (импульса) и момента количества движения (импульса). Когда одного госэксперта спросили в суде, импульсный или энергетический метод он использовал, он не нашелся, что сказать. Пояснил, что не различает. Сказал, что для этого же надо физику изучать.
Что же, давайте изучать, мы же не госэксперты…
Закон сохранения момента количества движения
Момент импульса – это импульс, умноженный на плечо. Приложим к автомобилю момент импульса, и он развернется относительно своего цента тяжести.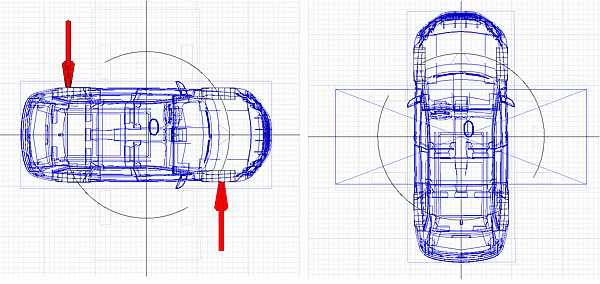
Обратите внимание, что сумма импульсов на рисунке выше равна нулю. Поэтому центр тяжести автомобиля никуда не сдвинулся. Но момент наши импульсы создали. И автомобиль получил некоторую скорость вращения.
На практике, в ДТП, трудно создать чистый момент, а чаще бывает, например, так
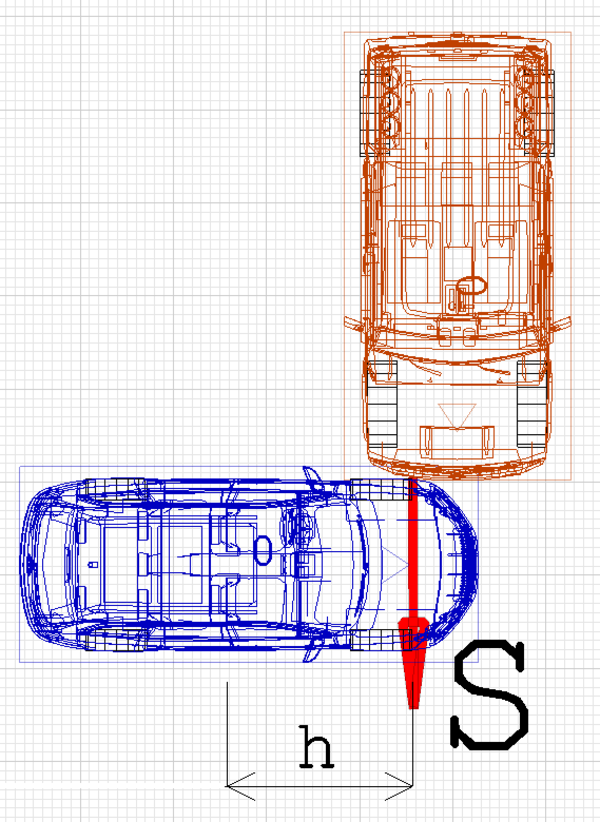
Здесь красный автомобиль действует на синий, и его действие и есть импульс силы S, а момент этого импульса есть hS. Второй автомобиль можно убрать, а импульс, действующий эксцентрично, заменить на такой же импульс в центре тяжести и его момент.
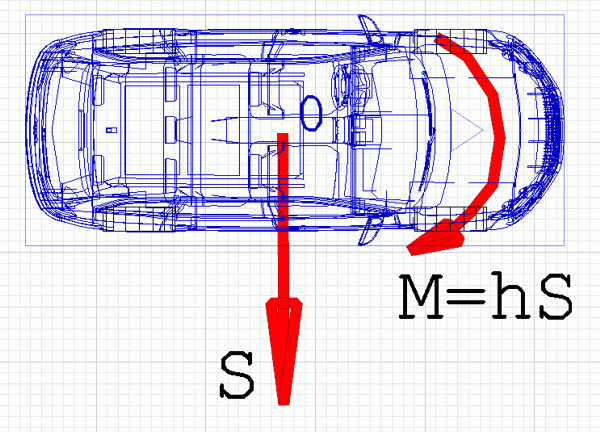
Теперь видно, что импульс в центре тяжести автомобиля может только отбросить автомобиль вправо, а его момент разворачивает автомобиль. Тогда зная угол разворота автомобиля, можно найти момент импульса. А зная плечо – и величину самого импульса. Величина же самого импульса – это есть масса второго, толкнувшего наш синий, красного автомобиля, умноженная на величину изменения (потери) им скорости в результате удара.
В результате удара синий автомобиль начнет вращаться. Скорость вращения его точки приложения импульса (вблизи левого переднего колеса) может быть вычислена как угловая скорость вращения синего автомобиля, умноженная на плечо импульса (на радиус вращения). Это и есть остаточная, после удара, скорость второго, красного автомобиля в момент разделения автомобилей.
Итак, теперь мы знаем величину изменения скорости красного автомобиля и его же остаточную скорость. Складываем их и получаем скорость красного автомобиля в момент столкновения. А сам красный автомобиль нам не нужен – пусть катится, куда хочет. Главное, чтобы синий автомобиль хоть где-нибудь наследил.
И, бывает, что следят такие бедолаги очень хорошо. В месте удара вмятина так себе, зато потом …
http://youtu.be/U7UpxgWJ29k
Самое время, читатель посмотреть приложенный к этой статье документ «Мерседес-БМВ», а потом вернуться сюда и продолжить чтение.
Все умные думают одинаково
Не думайте, читатель, что это сказано про экспертов с девиантным мышлением. Это я писал про других. А использование закона сохранения момента количества движения я уже показывал на «Праворубе» в статье «Устанавливаем скорости автомобилей в ДТП по их вращению». В суде, кстати, прошло как надо. Но рассмотрим более сложный и, так же реальный, случай в США.В лобовую сталкиваются грузовик и мотоцикл. В результате удара грузовик заносит. Надо установить скорость мотоцикла.

 Американцы, не обращаясь к экспертам в Российский Минюст (вот чудаки), а, применив закон сохранения момента импульса, установили изменение скорости вращения грузовика в результате удара, величину импульса удара, а отсюда – и скорость мотоцикла 31 милю в час в момент столкновения и 42 мили в час перед началом торможения.
Американцы, не обращаясь к экспертам в Российский Минюст (вот чудаки), а, применив закон сохранения момента импульса, установили изменение скорости вращения грузовика в результате удара, величину импульса удара, а отсюда – и скорость мотоцикла 31 милю в час в момент столкновения и 42 мили в час перед началом торможения. Их презентацию (на английском языке) можно посмотреть в приложении «Грузовик-мотоцикл», там все понятно, а сайт этих американских экспертов – здесь.
Смысл в их расчетах тот же, что и при столкновении Мерседеса с БМВ, с тем отличием, что грузовичок сам отворачивал (имел начальную скорость вращения), да и импульс действовал под косым углом к продольной оси грузовика.
Устанавливаем скорости Ауди и Хаммера в виртуальном ДТП
Пора перейти к более общему случаю, каковым является наше виртуальное ДТП. Сразу открою небольшой секрет – вычислять значения и направления импульсов и их моментов, как сделал я и американцы выше, в общем случае не надо. Достаточно записать систему уравнений закона сохранения момента импульса в проекциях на оси координат, и эти величины сократятся.Чтобы не пугать юристов сложными уравнениями к статье приложен фрагмент замечательной американской книги, очень хорошего учебника по реконструкции обстоятельств ДТП математическими методами. Нас интересует параграф 5.6, там показан вывод необходимых соотношений. Мы далее будем следовать обозначениям этого параграфа.
Нам понадобятся оба плеча импульса относительно центров тяжести автомобилей Ауди и Хаммер, как на рис.5.2 в учебнике. Их легко измерить по масштабной схеме.
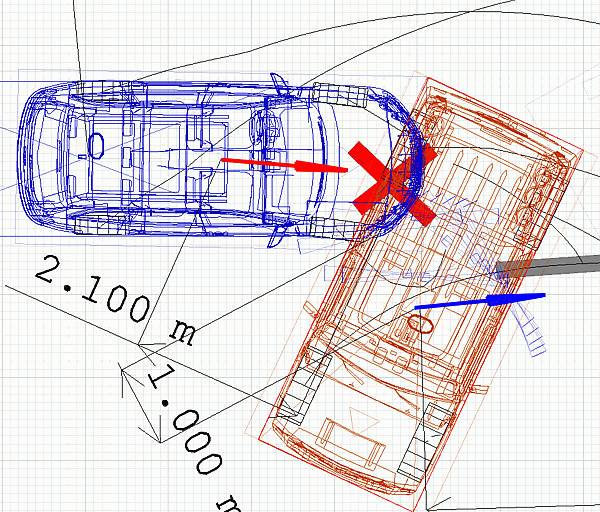
Как видно из рисунка выше, для Ауди величина плеча составляет 2.1 м, а угол плеча (размерной линии) с осью Х составляет 156 градусов. Для Хаммера, соответственно, 1 м и 118 градусов. Отсюда можно вычислить модули проекций обоих плеч на оси координат Х и Y.
Масса первого автомобиля, Ауди, составляет 1840 кг, масса второго автомобиля, Хаммера, составляет 3010 кг. Отношение массы Хаммера к массе Ауди составляет 1.64.
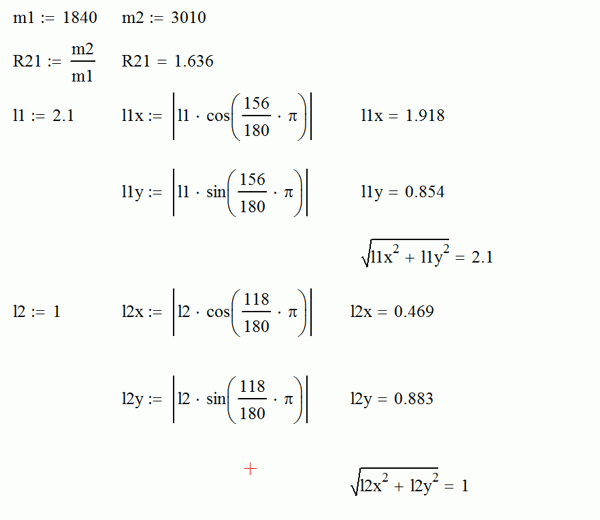
Угол направления скорости автомобиля Ауди с осью Х в момент столкновения был равен нулю, или A1i=0, угол направления скорости автомобиля Хаммер с осью Х в момент столкновения был равен -115 градусам, или A2i=-115.
В части 1 этой статьи я писал о том, что законы сохранения работают точно только тогда, когда направления всех векторов берутся непосредственно в месте столкновения, а не как направление от положения в момент столкновения к конечному положению.
При ударе Хаммер будет вращаться вокруг самой дальней точки опоры – переднего левого колеса. Если провести от переднего левого колеса Хаммера линию в его центр тяжести, то видно, что перпендикуляр к ней практически параллелен оси Х. Следовательно, скорость центра тяжести Хаммера в месте столкновения была направлена практически вдоль дороги. Для соблюдения закона сохранения количества движения сумма вектора скорости Хаммера, умноженного на соотношение масс 1.64, и вектора скорости Ауди должны составить вектор, направленный в сторону движения Ауди в момент столкновения – или горизонтально на рисунке выше. И если, например, вектор скорости Хаммера направлен, например, правее на 1.64 градуса, то вектор скорости Ауди должен быть направлен левее на один градус.
В нашем случае из рисунка выше понятно, что эти вектора близки по направлению к горизонтали, поэтому, не мудрствуя лукаво, считаем их углы с осью Х равными нулю. Не будем гоняться за абсолютной точностью.
На рисунке выше я показал стрелками направление движения центров тяжестей, которые показала компьютерная программа. Примерно так и есть.
Итак, углы направления скорости автомобиля Ауди и скорости автомобиля Хаммер с осью Х после удара равны нулю, или A1f=0 и A2f=0.
Угол разворота автомобиля Ауди в результате удара составил b1=131 градус. Угол разворота Хаммера составил b2=57 градусов.
Теперь надо определиться с местом, где мог закончиться разворот (занос) автомобиля Ауди при условии, что его центр тяжести после столкновения двигался под углом к оси Х, равным нулю или близким к нему. Крайний возможный вариант можно получить простым геометрическим построением.
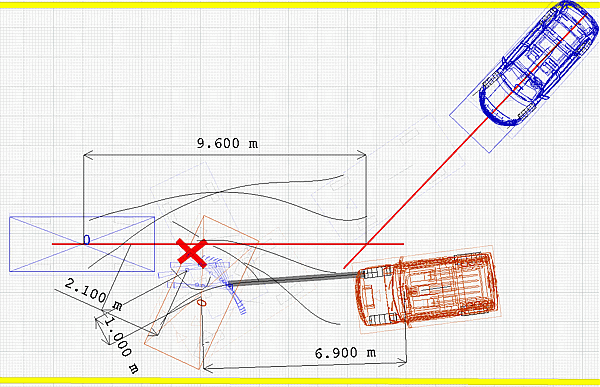
Как видно, отброс Ауди не мог превышать D1f=9.6 м. Для Хаммера – без вариантов D2f=6.9 м, так как Хаммер «привязан» к зафиксированному на схеме ДТП следу колеса.
По формулам 5.42 из учебника вычисляем приведенные (с учетом вращения) скорости автомобилей после удара (но уже в км/ч).

Далее все, что нужно, подставляем в систему уравнений 5.41 из учебника, и получаем результат после решения системы линейных уравнений: скорость Ауди в момент столкновения была около V1i=63.4 км/ч, скорость Хаммера была ноль, V2i=0.
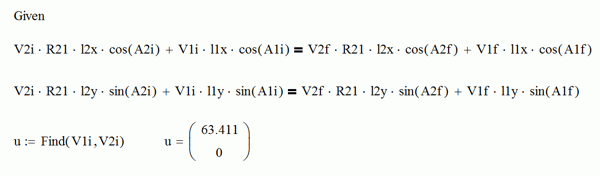 Откуда погрешность 3.4 км/ч? От предположения, что автомобиль Ауди двигался вращаясь аж 9.6м. Если использовать моделирующую программу, то можно сразу обнаружить, что Ауди, конечно, не может резко свернуть в конечное положение, и фактически это расстояние составляет около 7.8 м, что и было показано еще в части 1 этой статьи.
Откуда погрешность 3.4 км/ч? От предположения, что автомобиль Ауди двигался вращаясь аж 9.6м. Если использовать моделирующую программу, то можно сразу обнаружить, что Ауди, конечно, не может резко свернуть в конечное положение, и фактически это расстояние составляет около 7.8 м, что и было показано еще в части 1 этой статьи. Как видно, решить задачу с погрешностью менее 0.1 км/ч тоже реально.
Как видно, решить задачу с погрешностью менее 0.1 км/ч тоже реально.Подведем итоги
Законы вращательного движения тел, в том числе автомобилей, оказались пасынками для Российского Минюста. Они до сих пор этим самым Минюстом не апробированы и не утверждены. При этом сыны Минюста в судах в многочисленных городах и весях нашей необъятной России эти законы втихаря используют. Вспомните, как они машут руками, рассказывая как автомобиль подсудимого «летал туда-сюда», и, всегда, по «законам физики».Но законы физики имеют конкретное математическое выражение, так как математика – это язык физики. Всем понятно, куда я клоню. Все, что утверждают эксперты, должно быть результатом расчетов, а не голословным утверждением.
В начале этой части статьи показано, что наименьшая возможная скорости автомобиля в момент столкновения Ауди составляет 43.5 км/ч, предпоследнее решение дает наибольшую возможную скорость автомобиля Ауди в момент столкновения 63.4 км/ч. Может быть, этого достаточно. А если нет, надо проверить весь возможный интервал скоростей, и для каждой из них вычислить затраты энергии на деформацию автомобилей как разность их кинетической энергии до и после столкновения. Затем надо установить фактические затраты энергии на деформацию прочностными расчетами или с помощью данных краш-тестов. Только тогда будет получено решение, близкое к фактическому значению скорости.
Автор надеется, что эта статья будет полезна практикующим юристам.
Ваши голоса очень важны и позволяют выявлять действительно полезные материалы, интересные широкому кругу профессионалов. При этом бесполезные или откровенно рекламные тексты будут скрываться от посетителей и поисковых систем (Яндекс, Google и т.п.).
| 1. | Мерседес-БМВ | 1.9 MB | 44 | |||
| 2. | Грузовик-мотоцикл | 2.9 MB | 39 | |||
| 3. | Учебник | 478.7 KB | 47 |
Американцы, не обращаясь к экспертам в Российский Минюст (вот чудаки), а, применив закон сохранения момента импульса, установили изменение скорости вращения грузовика в результате удара, величину импульса удара, а отсюда – и скорость мотоцикла 31 милю в час в момент столкновения и 42 мили в час перед началом торможения.
Вот тебе и «тупые американцы»? Так над кем смеяться -то надо.
Ещё раз плюсую работу, уважаемый Владимир Николаевич!(bow)
Зато у нас есть духовные скрепы, а у них нет :D
Пошел вспоминать интегральные исчисления:)
Успеха, уважаемый Андрей Юрьевич! Но мы еще не дошли до тензорного анализа, без знания которого расчеты деформации автомобиля методом конечных элементов в PC-Crash превращаются просто в игру обезьяны на рояле.
Тензорный анализ — обобщение векторного анализа, раздел тензорного исчисления, изучающий дифференциальные операторы, действующие на алгебре тензорных полей D(M) дифференцируемого многообразия M. Рассматриваются также операторы, действующие на более общие, чем тензорные поля, геометрические объекты: тензорные плотности, дифференциальные формы со значениями в векторном расслоении и т.д.
Дерзайте, Андрей Юрьевич, так как после экспертных игр на рояле разгребать их симфонии придется нам с вами. :)
Спасибо за материалы .! «отдаю» для пользования нашему трасологу ( с Вашего позволения)))))....
Не вопрос, уважаемый Андрей Васильевич, на здоровье. :)
Уважаемый Владимир Николаевич, я конечно понимаю что для Вас такие расчеты семечки. Но для меня это полная абракадабра. Слишком научно изложено. Также не понятно если Мерседес перевернулся — то часть силы удара была направлена вверх, и на преодоление силу тяжести, часть энергии ушла и на это. Кроме того я так понял Мерседес на месте тоже не стоял, а ехал? Физика наука точная, но всех нюансов ДТП считаю что учесть никогда неполучиться. Как вы говорите невозможно точно определить когда колеса оказались заторможенными.
Уважаемый Константин Александрович, Мерседес тоже ехал. Чтобы его так закрутить, надо в поперечном направлении в его передней части приложить импульс, так? Но этот импульс и есть масса БМВ, умноженная на потерю скорости БМВ. А линейная скорость переда Мерса равна остаточной скорости БМВ.
для меня это полная абракадабраЯ вижу, что тут, на ПР, адвокаты в химии даже разбираются, ведут дела о наркотиках. А адвокату по ДТП надо в физике малость (на школьном уровне) разбираться, а то обманут. :)
Уважаемый Владимир Николаевич!
Солидарен с Вашим утверждением о том, что все утверждения экспертов должны иметь под собой расчёты, а не голословные утверждения. Это очевидно. Но вот суды принимают на веру и своё «внутреннее убеждение» выводы госэкспертов типа Гафарова (надеюсь, помните такого?), который без каких-либо расчётов и кинематики вывел: «С технической точки зрения столкновение произошло на встречной полосе».
Для таких судей наша критика — как брань на вороту — не виснет!
Для таких судей наша критика — как брань на вороту — не виснет!Значит, уважаемый Александр Эльмартович, их воротА и/или ворОта надо дегтем мазать. Это они тоже любят — на новые ворота смотреть, это ихнее, святое.
Ваши голоса очень важны и позволяют выявлять действительно полезные материалы, интересные широкому кругу профессионалов. При этом бесполезные или откровенно рекламные тексты будут скрываться от посетителей и поисковых систем (Яндекс, Google и т.п.).
В рамках адвокатской деятельности оказываю юр. помощь по многим вопросам.
Являюсь также профессиональным медиатором.
Защита по сложным уголовным экономическим делам.
Борьба с фальсификациями и незаконными методами расследования. Опыт, надёжность, добросовестность!
● Арбитраж. Банкротство. ФАС. Юридическое сопровождение вашего бизнеса.
● Юрист по ВЭД. Споры с ФТС. Международное право.
Дорого, но зато качественно. Все встречи и консультации, в т.ч. дистанционные только по предварительной записи.



Уважаемый Владимир Николаевич, спасибо за поучительную, наглядную и бесплатную лекцию по практической физике!
Учиться нам и учиться… однозначно в избранное :)
Правильно, Екатерина Александровна! Если юрист вооружен знаниями — значит он опасен для противника, и примеров тому на «Праворубе» тьма. (Y)