Найти юриста / адвоката / эксперта
Эта статья была опубликована в журнале Генеральной прокуратуры РФ «Законность», в № 5 за 2007 год. Она и сегодня актуальна, и будет актуальной еще долго. Причина — научный тупик, в который зашла автоэкспертиза, в стремлении к упрощению описания удара начав применять гипотезы для моделирования реальности.
Процесс пластической деформации деформируемого тердого тела описывается большой системой разнородных дифференциальных уравнений. Для ряда частных случаев их решения найдены математиками аналитически. Но общего аналитического решения нет.
Возможно, когда-нибудь и родится гений, который это сделает, и автоэксперты получат формулы для всех случаев удара и всех возможных повреждений машин. А пока выход один — вычислительная механика, которая успешно научилась перекладывать решение этих уравнений на компьютер.
В отличие от журнальной публикации здесь автор дополнил текст рисунками и некоторыми разъяснениями, выделенными курсивом.
Процессы интеграции с западноевропейскими странами привели к появлению и использованию в судебно-экспертной практике новых для России методов анализа ДТП, основанных на тех или иных математических моделях. Следователю или судье, не обладающими специальными познаниями в технических науках, подчас невозможно разобраться в вопросах допустимости применения нетрадиционных методик в судебном процессе, не имея четкого критерия их оценки. Такой критерий был предложен и научно обоснован автором статьи [Никонов В.Н. Допустимость математических моделей ДТП в судебном процессе. // Доклад на международной научно-практической конференции «Теория и практика судебной экспертизы в современных условиях». – М.: МГЮА, 2007].
Используемые в мировой практике методики анализа и реконструкции обстоятельств ДТП основываются на математических моделях, описывающих два основных процесса, происходящих в ДТП с автомобилями, – процесс движения и процесс удара. Оба процесса описываются моделями, построенными на научной основе, с использованием известных законов механики и базирующимися на тех или иных экспериментальных данных. Юристу, наблюдающему за дискуссией специалистов, невозможно разобраться в ее сущности, не имея четкого критерия оценки математических моделей ДТП. Если математические модели движения автомобиля не вызывают разногласий специалистов, то приемлемые для судебно-экспертных исследований модели удара автомобилей требуют классификации и оценки.
Математическая модель – это формализованное описание выявленных признаков объекта экспертного исследования [Аверьянова Т.В. Судебная экспертиза: курс общей теории. – М.: Норма, 2006. – 480с.]. В применяемых в мировой судебно-экспертной практике методиках математическая модель удара строится двумя основными способами. Первый – феноменологическое исследование автомобиля как единого целого, когда он представлен только своей наружной оболочкой, а свойства его внутренней структуры переносятся на свойства его оболочки. Второй – построение математических моделей отдельных наружных и внутренних элементов конструкции, составляющих автомобиль, с их последующей интеграцией в единую модель. В первом способе построения математической модели источником фактических данных служат результаты испытаний автомобиля на удар – краш-тесты, во втором – результаты испытаний материалов, из которых изготовлены элементы конструкции автомобиля.
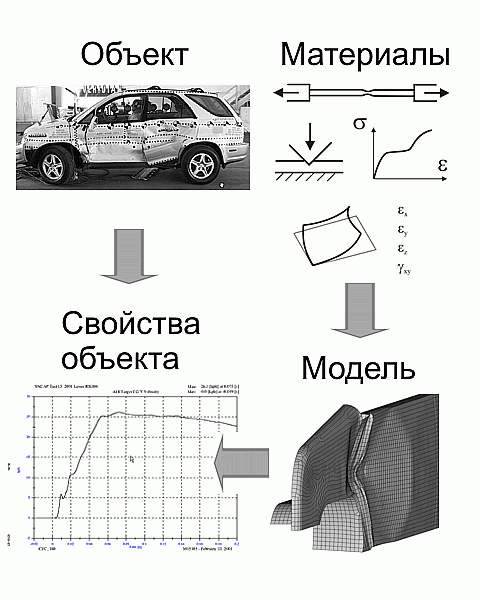Оба способа построения модели научны, так как они базируются на фактических экспериментальных данных, но научны ли полученные математические модели? Для ответа на этот вопрос необходимо применить понятия интерполяционной и экстраполяционной модели.
При исследовании некоторого объекта устанавливаются реакции этого объекта на те или иные воздействия на него. Например, для автомобиля устанавливается зависимость величины его замедления при торможении на некотором дорожном покрытии (реакция) при той или иной загрузке автомобиля (воздействие). Интервал от наименьшего до наибольшего значения воздействия на объект составляет область определения, на которой стоится математическая модель, являющаяся при таком подходе интерполяционной – предназначенной для вычисления реакции при тех или иных значениях воздействий из области определения. Так, например, экспериментальное измерение значений замедления тормозящего снаряженного автомобиля, его же с 50% и 100% загрузкой при некоторых дорожных условиях позволяет с достаточной для судебно-экспертного исследования точностью вычислить значение замедления, например, при 70% загрузке. Однако то, что значение замедления падает с ростом загрузки автомобиля, не означает, что при некоторой загрузке выше 100% значение замедления станет равным нулю и заторможенный автомобиль никогда не остановится. Математическая модель, вычисляющая величину реакции объекта при величине воздействия, находящегося вне области определения, является экстраполяционной – предназначенной для прогнозирования величины реакции на основе некоторой гипотезы, точность результатов которой может быть установлена только статистически при большом числе испытаний, а точность результата в конкретном испытании неизвестна.
Экстраполяцию, как нарушение логической цепочки доказательства, взгляд специалиста нередко замечает в заключениях автоэкспертов, что, вероятно, не заметно адвокатам. Мокрый асфальт – могло занести – … –занесло. Или, произошел слабый удар (касание) – изменилось курсовое направление – выезд в кювет. И т.д. Экстраполяция заключается в незаметной подмене результата расчета (часто, из-за невозможности или неумения его произвести) наукоподобными, подчас ложными, посылками, принимающимися как аксиома и экспертом, и затем юристами.
Правомерность того или иного средства или метода в судебной экспертизе должна определяться исходя из общих принципов допустимости научно-технических средств и методов в судопроизводстве [Россинская Е.Р. Судебная экспертиза в гражданском, арбитражном, административном и уголовном процессе. – М.: Норма, 2005. – 656с.], среди которых для математических моделей главную роль играют их научность, надежность и точность результатов. Поэтому вопрос о допустимости математических моделей ДТП в судебном процессе является актуальным.
Традиционные методики автотехнических экспертиз, в том числе и методика, применяемая СЭУ МЮ и МВД РФ, не содержат моделей удара автомобилей. Их модель основана на использовании закона трения Кулона и частичном использовании закона сохранения энергии, когда часть кинетической энергии движущегося автомобиля можно определить по длине его тормозного пути. Эта модель является интерполяционной, так как значения замедления автомобилей для всех возможных дорожных покрытий определены экспериментально с 95%-ым уровнем обеспеченности [Суворов Ю.Б. Судебная дорожно-транспортная экспертиза. Судебно-экспертная оценка действий водителей и других лиц, ответственных за обеспечение безопасности дорожного движения, на участках ДТП: Учебное пособие. – М.: «Экзамен», «Право и закон», 2003. – 208с.]. Интерполяционность традиционной модели и обуславливает категоричность ее результатов, и, следовательно, допустимость в качестве доказательства в судебном процессе.
Автоэксперт, например, по длине тормозного следа установил, что скорость автомобиля перед началом торможения была не менее 70км/ч. Этот вывод, безусловно, категоричен. Но далее за его логикой нужно внимательно следить, так как часто эти 70км/ч возводятся в абсолют, и дорожно-транспортная ситуация не оценивается для возможных скоростей этого автомобиля 80, 90, …, 150, … км/ч.
Ограниченность возможностей традиционной модели привела к созданию методик, включающих, кроме модели движения, и модель удара автомобилей. Эти методики реализованы в виде множества компьютерных программ, как, например, CARAT и PC-Crash. Их использование в странах Запада является стандартным приёмом для моделирования механизма ДТП и его визуализации, что позволяет не только всесторонне производить исследование, но и более понятно и наглядно представить его результаты [Митунявичус В. К вопросу о точности расчетов и категоричности выводов при производстве автотехнических экспертиз. // Доклад на международной научно-практической конференции «Проблемные вопросы развития современных методологий экспертного анализа ДТП. Возможности экспертных исследований в установлении фальсификации ДТП». DEKRA (Германия) и ДЕКРА Эксперт (Украина). –Киев, 2006]. Модель удара в этих методиках базируется на двух гипотезах – гипотезе Кудлиха-Слибара [Никонов В.Н. Гипотеза Кудлиха-Слибара: миф и реальность. // Официальный сайт Центра независимой экспертизы на автомобильном транспорте. – Самара, 2006. – http://www.cneat.ru/kudl.htm] и гипотезе трехсторонней унифицированной жесткости CRASH [Никонов В.Н. Метод Delta-V: анализ и выводы. // Официальный сайт Центра независимой экспертизы на автомобильном транспорте. – Самара, 2006. – http://www.cneat.ru/nikonov-delta3.htm]. Так как наука обычно называет методы, применяющие упрощающие гипотезы, инженерными, то далее и эти модели ДТП так же будем называть инженерными. Хотя сам факт использования гипотез уже является признаком экстраполяционности модели удара, содержание этих гипотез следует рассмотреть глубже.
Гипотеза Кудлиха-Слибара предложена авторами в 1966 году. Она упрощает физический механизм удара автомобилей, полагая, что удар происходит мгновенно и в некоторой общей для деформированных автомобилей «импульсной» точке, находящейся на поверхности их раздела. Суть гипотезы – замена изменяющейся по величине и направлению силы взаимодействия импульсом, одинаковым для столкнувшихся автомобилей по величине и, в силу равенства действия противодействию, противоположным по направлению. Не учитываемый при этом момент импульса компенсируется подбором экспертом точки импульса и направления импульса так, чтобы максимально точно обеспечить фактическую траекторию движения автомобилей после удара. Погрешность, возникающая из-за этого упрощения законов механики, не контролируема и может быть оценена только статистически. Но суть гипотезы дает основания утверждать, что ошибка расчета будет больше, если длительность столкновения автомобилей велика – их путь за время контакта сопоставим с расстоянием, пройденным ими с момента столкновения до конечного положения. Применение импульса так же исключает возможность анализа ДТП в случаях, когда точка импульса «мигрирует» по автомобилю в течение времени контакта, как, например, при касательном столкновении.
Справка. Импульсом (или количеством движения) называется произведение величины силы на время ее действия, или, что одно и то же, произведение массы тела на изменение его скорости. То есть изменение скорости равно частному от деления величины импульса на массу тела. А величину импульса можно определить, не зная величину силы и время ее действия. Простой пример ошибки импульсного метода следующий. Пусть во время движения на правую часть Жигулей спереди справа налево действует сила 1000кг в течении 0.1с, потом 100кг в течении 1с. Величина, точка приложения к автомобилю и направление обоих импульсов одинаково. Но в первом случае автомобиль изменит курсовое направление, так как силы достаточно для сдвига передних колес влево, а во втором – нет, в худшем случае на крыле будет только вмятина.
В общем случае уравнений законов сохранения импульса и его момента недостаточно для решения задачи удара. Поэтому инженерными моделями вводится дополнительное уравнение, содержащее коэффициент восстановления скорости после удара, который, по сути, является мерой потери кинетической энергии столкнувшихся автомобилей на деформацию их конструкций при ударе. Но и это дополнительное уравнение вновь вводится в математическую модель на основе гипотезы – гипотезы трехсторонней унифицированной жесткости, ставшей известной с выходом в 1976 году в США компьютерной программы анализа ДТП CRASH (от Calspan Reconstruction of Accident Speeds on the Highway – реконструкция скоростных столкновений на дорогах корпорации Calspan) [McHenry R.R. User’s Manual for the CRASH Computer Program. // NTIS, 1976. – Pb № 252115].
Напомним, что жесткостью конструкции называется отношение величины силы, которую надо приложить для образования деформации, к величине этой деформации. Гипотеза унифицированной жесткости основана на предположении, что для автомобиля достаточно определить три величины жесткости – жесткость переда, жесткость зада и жесткость боковых сторон. Эти жесткости не зависят от места приложения нагрузки и характера деформации, постоянны при деформации автомобиля, а их вычисление может быть проведено на основе данных краш-теста автомобиля на фронтальный или боковой удар о жесткий барьер. Далее полагается, что все существующие модели автомобилей можно разделить на конечное число категорий (для легковых автомобилей выделено 7 категорий) в зависимости от массы геометрических параметров, и для каждой категории достаточно определить усредненные значения указанных трех жесткостей [Никонов В.Н. Оценка соответствия деформаций транспортных средств инженерными методами. // Страховое дело. – 2005. – №10. – С.41-45].
Допущения гипотезы унифицированной трехсторонней жесткости приводят к экстраполяционности инженерной модели удара вследствие выхода за пределы области определения эксперимента по нижеследующим причинам.
На рисунке выше — фрагмент документации по CRASH-3. Знающий английский увидит, что авторы предупреждают о неточности метода, пишут о величине погрешности определения скорости этим методом в среднем более 40%. При этом следует отметить, что если условия ДТП близки (что такое «близки» здесь не обсуждается) к условиям краш-теста, то статистическая погрешность не превышает 10%.
Таким образом, инженерные модели, основанные на гипотезах, содержат множественную экстраполяцию за пределы области экспериментального определения параметров, в силу чего инженерные модели являются по своей сути вероятностными и не отвечают требованиям допустимости в судебном процессе. Этот вывод подтверждается и тем, что, по данным самих разработчиков, гипотеза трехсторонней унифицированной жесткости дает в отдельных экспериментах более чем 40%-ю погрешность определения скорости ТС [CRASH-3 Technical manual. // U.S. Department of Transportation. National Highway Traffic Safety Administration. National Center for Statistics and Analysis Accident Investigation Division. – 1986]. Использование же этой гипотезы в сочетании с гипотезой Кудлиха-Слибара может приводить к множеству возможных решений, когда одинаковое движение автомобилей после удара может определяться широким спектром сочетаний возможных параметров их движения в момент столкновения [Cliff W.E., Moser A. Reconstruction of Twenty Staged Collisions with PC-Crash’s Optimizer. // SAE Paper №2001-01-05-07].
На рисунке ниже слева вверху показан некий металлический объект – коробка с двумя продольными ребрами жесткости. Это несколько напоминает кузов автомобиля, но форма, конечно, более простая. Далее последовательно показаны результаты удара коробки левой передней частью в стену, когда углы между продольной осью коробки и перпендикуляром к стенке составляют 0, 30, 60 и 90 градусов. А внизу приведены соответствующие графики сил взаимодействия. Они хорошо демонстрируют одну из причин погрешности гипотезы трехсторонней жесткости CRASH-3 — сила сопротивления деформированию зависит от ориентации вектора скорости коробки.
Расчет сделан методом конечных элементов.
Задача замены гипотезы Кудлиха-Слибара и гипотезы трехсторонней унифицированной жесткости в инженерной модели может быть успешно решена использованием научно разработанного и широко апробированного мировой наукой и практикой метода вычислительной механики – метода конечных элементов (МКЭ), имеющего в России нормативный характер, что закреплено как ГОСТ, так и соответствующим стандартом ISO [ГОСТ Р 50-54-42-88 «Расчеты и испытания на прочность. Метод конечных элементов и программы расчета на ЭВМ пространственных элементов конструкций в упругопластической области деформирования». ГОСТ ISO 10303-104:2000 «Системы промышленной автоматизации и интеграция. Представление данных о продукции и обмен данными. Часть 104. Интегрированный прикладной источник: анализ конечных элементов»]. При этом интегрированная математическая модель автомобиля или его части, которая получила деформации в ДТП, строится на основе данных о геометрии элементов конструкции этой части, механических свойствах материалов этих элементов конструкции, и фактических данных о характере и величине полученных при ударе деформаций. Этих исходных данных достаточно для исследования объекта моделирования в самых широких пределах области определения возможных воздействий, изменяющихся как во времени, так и пространстве. Использование в расчетах возможных наибольших или возможных наименьших механических характеристик материалов элементов конструкций ТС всегда дает возможность получить технически возможные крайние параметры удара, что дает возможность получить категоричные выводы о параметрах движения автомобилей в момент их столкновения. Отметим, что достоверность МКЭ-модели удара признается и разработчиками инженерных моделей, и применяется ими как в экспертной практике, так и для проверки собственных упрощенных инженерных моделей [Day T.D., York A.R. Method for simulating collisions. // United States Patent №6195625].
Допустимость и объективность численной МКЭ-модели удара обусловлена тем, что модель строится на основе феноменологических исследований простейших ее составляющих – конечных элементов, – область определения воздействий на которые является полной и ограничивается только их разрушением. Описание конечных элементов методами механики деформируемого твердого тела не накладывает никаких ограничений на последовательность приложения воздействий в пространстве или времени, что делает МКЭ-модель удара интерполяционной и лишенной самой возможности экстраполяции за пределы области определения возможных воздействий при любом напряженно-деформированном состоянии.
Замечательные свойства МКЭ: 1) Сходимость метода – метод имеет собственную возможность оценки погрешности решения задачи. 2) При заданных граничных условиях будет найдено решение, соответствующее минимуму расхода энергии. 3)Неполнота модели ТС гарантирует получение возможных наименьших затрат энергии. 4) Из-за использования упруго-идеальнопластической модели материала результат расчета не зависит от последовательности деформирования.
Таким образом, классификация математических моделей ДТП с точки зрения их интерполяционности выглядит следующим образом:
Исторически сложилось так, что Российская судебная экспертиза не применяла и не применяет инженерные модели в практике судебных экспертных исследований. Однако бурное развитие мощности доступной вычислительной техники дает возможность перешагнуть этот этап развития и сразу перейти к использованию более наукоёмких, но допустимых в судебном процессе численных математических моделей удара на основе методов вычислительной механики.
Процесс пластической деформации деформируемого тердого тела описывается большой системой разнородных дифференциальных уравнений. Для ряда частных случаев их решения найдены математиками аналитически. Но общего аналитического решения нет.
Возможно, когда-нибудь и родится гений, который это сделает, и автоэксперты получат формулы для всех случаев удара и всех возможных повреждений машин. А пока выход один — вычислительная механика, которая успешно научилась перекладывать решение этих уравнений на компьютер.
В отличие от журнальной публикации здесь автор дополнил текст рисунками и некоторыми разъяснениями, выделенными курсивом.
Процессы интеграции с западноевропейскими странами привели к появлению и использованию в судебно-экспертной практике новых для России методов анализа ДТП, основанных на тех или иных математических моделях. Следователю или судье, не обладающими специальными познаниями в технических науках, подчас невозможно разобраться в вопросах допустимости применения нетрадиционных методик в судебном процессе, не имея четкого критерия их оценки. Такой критерий был предложен и научно обоснован автором статьи [Никонов В.Н. Допустимость математических моделей ДТП в судебном процессе. // Доклад на международной научно-практической конференции «Теория и практика судебной экспертизы в современных условиях». – М.: МГЮА, 2007].
Используемые в мировой практике методики анализа и реконструкции обстоятельств ДТП основываются на математических моделях, описывающих два основных процесса, происходящих в ДТП с автомобилями, – процесс движения и процесс удара. Оба процесса описываются моделями, построенными на научной основе, с использованием известных законов механики и базирующимися на тех или иных экспериментальных данных. Юристу, наблюдающему за дискуссией специалистов, невозможно разобраться в ее сущности, не имея четкого критерия оценки математических моделей ДТП. Если математические модели движения автомобиля не вызывают разногласий специалистов, то приемлемые для судебно-экспертных исследований модели удара автомобилей требуют классификации и оценки.
Математическая модель – это формализованное описание выявленных признаков объекта экспертного исследования [Аверьянова Т.В. Судебная экспертиза: курс общей теории. – М.: Норма, 2006. – 480с.]. В применяемых в мировой судебно-экспертной практике методиках математическая модель удара строится двумя основными способами. Первый – феноменологическое исследование автомобиля как единого целого, когда он представлен только своей наружной оболочкой, а свойства его внутренней структуры переносятся на свойства его оболочки. Второй – построение математических моделей отдельных наружных и внутренних элементов конструкции, составляющих автомобиль, с их последующей интеграцией в единую модель. В первом способе построения математической модели источником фактических данных служат результаты испытаний автомобиля на удар – краш-тесты, во втором – результаты испытаний материалов, из которых изготовлены элементы конструкции автомобиля.
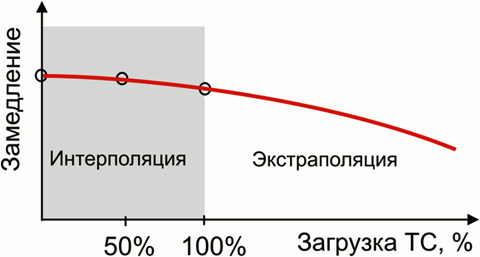
Оба способа построения модели научны, так как они базируются на фактических экспериментальных данных, но научны ли полученные математические модели? Для ответа на этот вопрос необходимо применить понятия интерполяционной и экстраполяционной модели. При исследовании некоторого объекта устанавливаются реакции этого объекта на те или иные воздействия на него. Например, для автомобиля устанавливается зависимость величины его замедления при торможении на некотором дорожном покрытии (реакция) при той или иной загрузке автомобиля (воздействие). Интервал от наименьшего до наибольшего значения воздействия на объект составляет область определения, на которой стоится математическая модель, являющаяся при таком подходе интерполяционной – предназначенной для вычисления реакции при тех или иных значениях воздействий из области определения. Так, например, экспериментальное измерение значений замедления тормозящего снаряженного автомобиля, его же с 50% и 100% загрузкой при некоторых дорожных условиях позволяет с достаточной для судебно-экспертного исследования точностью вычислить значение замедления, например, при 70% загрузке. Однако то, что значение замедления падает с ростом загрузки автомобиля, не означает, что при некоторой загрузке выше 100% значение замедления станет равным нулю и заторможенный автомобиль никогда не остановится. Математическая модель, вычисляющая величину реакции объекта при величине воздействия, находящегося вне области определения, является экстраполяционной – предназначенной для прогнозирования величины реакции на основе некоторой гипотезы, точность результатов которой может быть установлена только статистически при большом числе испытаний, а точность результата в конкретном испытании неизвестна.
Экстраполяцию, как нарушение логической цепочки доказательства, взгляд специалиста нередко замечает в заключениях автоэкспертов, что, вероятно, не заметно адвокатам. Мокрый асфальт – могло занести – … –занесло. Или, произошел слабый удар (касание) – изменилось курсовое направление – выезд в кювет. И т.д. Экстраполяция заключается в незаметной подмене результата расчета (часто, из-за невозможности или неумения его произвести) наукоподобными, подчас ложными, посылками, принимающимися как аксиома и экспертом, и затем юристами.
Правомерность того или иного средства или метода в судебной экспертизе должна определяться исходя из общих принципов допустимости научно-технических средств и методов в судопроизводстве [Россинская Е.Р. Судебная экспертиза в гражданском, арбитражном, административном и уголовном процессе. – М.: Норма, 2005. – 656с.], среди которых для математических моделей главную роль играют их научность, надежность и точность результатов. Поэтому вопрос о допустимости математических моделей ДТП в судебном процессе является актуальным.
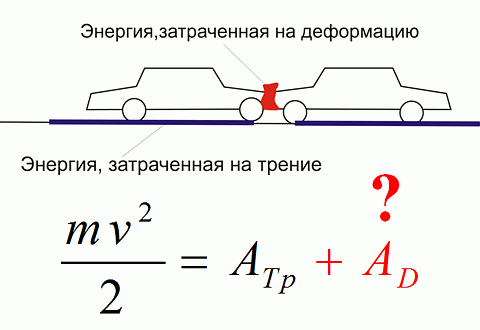
Традиционные методики автотехнических экспертиз, в том числе и методика, применяемая СЭУ МЮ и МВД РФ, не содержат моделей удара автомобилей. Их модель основана на использовании закона трения Кулона и частичном использовании закона сохранения энергии, когда часть кинетической энергии движущегося автомобиля можно определить по длине его тормозного пути. Эта модель является интерполяционной, так как значения замедления автомобилей для всех возможных дорожных покрытий определены экспериментально с 95%-ым уровнем обеспеченности [Суворов Ю.Б. Судебная дорожно-транспортная экспертиза. Судебно-экспертная оценка действий водителей и других лиц, ответственных за обеспечение безопасности дорожного движения, на участках ДТП: Учебное пособие. – М.: «Экзамен», «Право и закон», 2003. – 208с.]. Интерполяционность традиционной модели и обуславливает категоричность ее результатов, и, следовательно, допустимость в качестве доказательства в судебном процессе.
Автоэксперт, например, по длине тормозного следа установил, что скорость автомобиля перед началом торможения была не менее 70км/ч. Этот вывод, безусловно, категоричен. Но далее за его логикой нужно внимательно следить, так как часто эти 70км/ч возводятся в абсолют, и дорожно-транспортная ситуация не оценивается для возможных скоростей этого автомобиля 80, 90, …, 150, … км/ч.
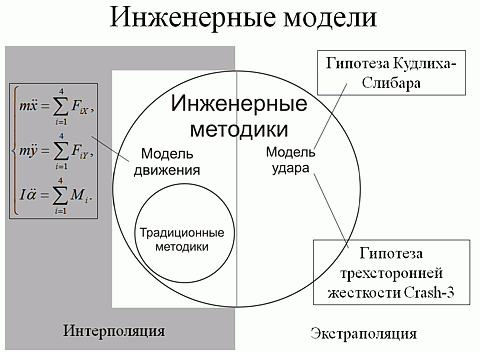
Ограниченность возможностей традиционной модели привела к созданию методик, включающих, кроме модели движения, и модель удара автомобилей. Эти методики реализованы в виде множества компьютерных программ, как, например, CARAT и PC-Crash. Их использование в странах Запада является стандартным приёмом для моделирования механизма ДТП и его визуализации, что позволяет не только всесторонне производить исследование, но и более понятно и наглядно представить его результаты [Митунявичус В. К вопросу о точности расчетов и категоричности выводов при производстве автотехнических экспертиз. // Доклад на международной научно-практической конференции «Проблемные вопросы развития современных методологий экспертного анализа ДТП. Возможности экспертных исследований в установлении фальсификации ДТП». DEKRA (Германия) и ДЕКРА Эксперт (Украина). –Киев, 2006]. Модель удара в этих методиках базируется на двух гипотезах – гипотезе Кудлиха-Слибара [Никонов В.Н. Гипотеза Кудлиха-Слибара: миф и реальность. // Официальный сайт Центра независимой экспертизы на автомобильном транспорте. – Самара, 2006. – http://www.cneat.ru/kudl.htm] и гипотезе трехсторонней унифицированной жесткости CRASH [Никонов В.Н. Метод Delta-V: анализ и выводы. // Официальный сайт Центра независимой экспертизы на автомобильном транспорте. – Самара, 2006. – http://www.cneat.ru/nikonov-delta3.htm]. Так как наука обычно называет методы, применяющие упрощающие гипотезы, инженерными, то далее и эти модели ДТП так же будем называть инженерными. Хотя сам факт использования гипотез уже является признаком экстраполяционности модели удара, содержание этих гипотез следует рассмотреть глубже.
Гипотеза Кудлиха-Слибара предложена авторами в 1966 году. Она упрощает физический механизм удара автомобилей, полагая, что удар происходит мгновенно и в некоторой общей для деформированных автомобилей «импульсной» точке, находящейся на поверхности их раздела. Суть гипотезы – замена изменяющейся по величине и направлению силы взаимодействия импульсом, одинаковым для столкнувшихся автомобилей по величине и, в силу равенства действия противодействию, противоположным по направлению. Не учитываемый при этом момент импульса компенсируется подбором экспертом точки импульса и направления импульса так, чтобы максимально точно обеспечить фактическую траекторию движения автомобилей после удара. Погрешность, возникающая из-за этого упрощения законов механики, не контролируема и может быть оценена только статистически. Но суть гипотезы дает основания утверждать, что ошибка расчета будет больше, если длительность столкновения автомобилей велика – их путь за время контакта сопоставим с расстоянием, пройденным ими с момента столкновения до конечного положения. Применение импульса так же исключает возможность анализа ДТП в случаях, когда точка импульса «мигрирует» по автомобилю в течение времени контакта, как, например, при касательном столкновении.
Справка. Импульсом (или количеством движения) называется произведение величины силы на время ее действия, или, что одно и то же, произведение массы тела на изменение его скорости. То есть изменение скорости равно частному от деления величины импульса на массу тела. А величину импульса можно определить, не зная величину силы и время ее действия. Простой пример ошибки импульсного метода следующий. Пусть во время движения на правую часть Жигулей спереди справа налево действует сила 1000кг в течении 0.1с, потом 100кг в течении 1с. Величина, точка приложения к автомобилю и направление обоих импульсов одинаково. Но в первом случае автомобиль изменит курсовое направление, так как силы достаточно для сдвига передних колес влево, а во втором – нет, в худшем случае на крыле будет только вмятина.
В общем случае уравнений законов сохранения импульса и его момента недостаточно для решения задачи удара. Поэтому инженерными моделями вводится дополнительное уравнение, содержащее коэффициент восстановления скорости после удара, который, по сути, является мерой потери кинетической энергии столкнувшихся автомобилей на деформацию их конструкций при ударе. Но и это дополнительное уравнение вновь вводится в математическую модель на основе гипотезы – гипотезы трехсторонней унифицированной жесткости, ставшей известной с выходом в 1976 году в США компьютерной программы анализа ДТП CRASH (от Calspan Reconstruction of Accident Speeds on the Highway – реконструкция скоростных столкновений на дорогах корпорации Calspan) [McHenry R.R. User’s Manual for the CRASH Computer Program. // NTIS, 1976. – Pb № 252115].
Напомним, что жесткостью конструкции называется отношение величины силы, которую надо приложить для образования деформации, к величине этой деформации. Гипотеза унифицированной жесткости основана на предположении, что для автомобиля достаточно определить три величины жесткости – жесткость переда, жесткость зада и жесткость боковых сторон. Эти жесткости не зависят от места приложения нагрузки и характера деформации, постоянны при деформации автомобиля, а их вычисление может быть проведено на основе данных краш-теста автомобиля на фронтальный или боковой удар о жесткий барьер. Далее полагается, что все существующие модели автомобилей можно разделить на конечное число категорий (для легковых автомобилей выделено 7 категорий) в зависимости от массы геометрических параметров, и для каждой категории достаточно определить усредненные значения указанных трех жесткостей [Никонов В.Н. Оценка соответствия деформаций транспортных средств инженерными методами. // Страховое дело. – 2005. – №10. – С.41-45].
Допущения гипотезы унифицированной трехсторонней жесткости приводят к экстраполяционности инженерной модели удара вследствие выхода за пределы области определения эксперимента по нижеследующим причинам.
- Гипотезой игнорируется, что на сторонах автомобиля всегда имеются места, где жесткость существенно отличается от средней жесткости стороны автомобиля. Так, например, жесткость в середине двери автомобиля меньше жесткости в районе его стоек. Тогда, например, расчет вмятины на двери на базе средней жесткости даст заведомо большие величину затрат энергии на деформацию и деформирующей силы, а расчет деформации сочленения стойки с порогом автомобиля – заведомо меньшие величины.
- Гипотезой игнорируется, что во время деформации автомобиля сила сопротивления конструкции постоянно изменяется далеко не по линейному закону, а, следовательно, жесткость стороны автомобиля не постоянна, а является функцией деформации. Это, в частности, следует из результатов краш-тестов, во время которых производится прямое измерение зависимостей сил сопротивления различных частей конструкции от времени. Тогда расчет деформаций на базе средней жесткости, полученных в условиях, близких к краш-тесту, но при меньшей скорости приведет к непрогнозируемой ошибке, для исключения которой эксперту необходимо иметь не усредненные коэффициенты жесткости, а экспериментальные или полученные прочностным расчетом зависимости силы сопротивления автомобиля от деформации или от времени.
- Гипотезой игнорируется, что краш-тесты проводятся при скоростях удара до 64км/ч, а фактические столкновения в ДТП могут происходить при больших, чем 64км/ч, энергетически эквивалентных скоростях. Этот случай является прямой экстраполяцией за пределы эксперимента.
- Гипотезой игнорируется, что краш-тесты проводятся для условий фронтального или бокового удара автомобиля о барьер, а фактические столкновения в ДТП могут происходить под произвольными углами. Механикой давно установлено, что двух экспериментов во взаимно перпендикулярных направлениях достаточно для определения свойств только ортотропных объектов, имеющих ярко выраженные структурные элементы в одном направлении (ортотропный материал – это, например, слоистая фанера). Так как структура автомобиля гораздо сложнее, перенос результатов экспериментов на удар под произвольным углом не научен и является экстраполяцией за пределы экспериментально установленного пути деформации, на котором происходит расход энергии.
- Гипотезой полагается, что деформации автомобиля хотя и могут быть произвольными в горизонтальной плоскости, но одинаковы по высоте. Тем самым игнорируется локализация деформаций, и в случаях локализации деформаций в нижней, верхней или иной части автомобиля усреднение по высоте осуществляется экспертом субъективно, что не исключает возможности экстраполяции жесткости за пределы эксперимента.
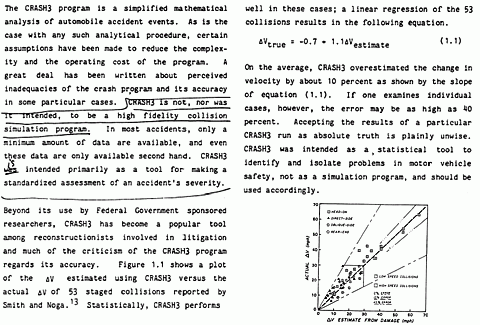На рисунке выше — фрагмент документации по CRASH-3. Знающий английский увидит, что авторы предупреждают о неточности метода, пишут о величине погрешности определения скорости этим методом в среднем более 40%. При этом следует отметить, что если условия ДТП близки (что такое «близки» здесь не обсуждается) к условиям краш-теста, то статистическая погрешность не превышает 10%. Таким образом, инженерные модели, основанные на гипотезах, содержат множественную экстраполяцию за пределы области экспериментального определения параметров, в силу чего инженерные модели являются по своей сути вероятностными и не отвечают требованиям допустимости в судебном процессе. Этот вывод подтверждается и тем, что, по данным самих разработчиков, гипотеза трехсторонней унифицированной жесткости дает в отдельных экспериментах более чем 40%-ю погрешность определения скорости ТС [CRASH-3 Technical manual. // U.S. Department of Transportation. National Highway Traffic Safety Administration. National Center for Statistics and Analysis Accident Investigation Division. – 1986]. Использование же этой гипотезы в сочетании с гипотезой Кудлиха-Слибара может приводить к множеству возможных решений, когда одинаковое движение автомобилей после удара может определяться широким спектром сочетаний возможных параметров их движения в момент столкновения [Cliff W.E., Moser A. Reconstruction of Twenty Staged Collisions with PC-Crash’s Optimizer. // SAE Paper №2001-01-05-07].
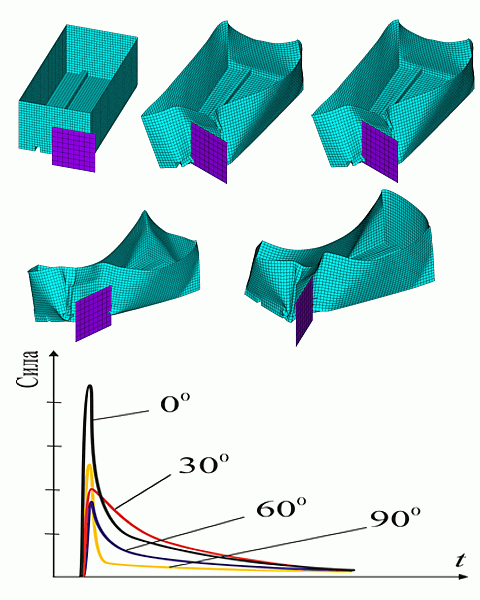
На рисунке ниже слева вверху показан некий металлический объект – коробка с двумя продольными ребрами жесткости. Это несколько напоминает кузов автомобиля, но форма, конечно, более простая. Далее последовательно показаны результаты удара коробки левой передней частью в стену, когда углы между продольной осью коробки и перпендикуляром к стенке составляют 0, 30, 60 и 90 градусов. А внизу приведены соответствующие графики сил взаимодействия. Они хорошо демонстрируют одну из причин погрешности гипотезы трехсторонней жесткости CRASH-3 — сила сопротивления деформированию зависит от ориентации вектора скорости коробки.
Расчет сделан методом конечных элементов.
Задача замены гипотезы Кудлиха-Слибара и гипотезы трехсторонней унифицированной жесткости в инженерной модели может быть успешно решена использованием научно разработанного и широко апробированного мировой наукой и практикой метода вычислительной механики – метода конечных элементов (МКЭ), имеющего в России нормативный характер, что закреплено как ГОСТ, так и соответствующим стандартом ISO [ГОСТ Р 50-54-42-88 «Расчеты и испытания на прочность. Метод конечных элементов и программы расчета на ЭВМ пространственных элементов конструкций в упругопластической области деформирования». ГОСТ ISO 10303-104:2000 «Системы промышленной автоматизации и интеграция. Представление данных о продукции и обмен данными. Часть 104. Интегрированный прикладной источник: анализ конечных элементов»]. При этом интегрированная математическая модель автомобиля или его части, которая получила деформации в ДТП, строится на основе данных о геометрии элементов конструкции этой части, механических свойствах материалов этих элементов конструкции, и фактических данных о характере и величине полученных при ударе деформаций. Этих исходных данных достаточно для исследования объекта моделирования в самых широких пределах области определения возможных воздействий, изменяющихся как во времени, так и пространстве. Использование в расчетах возможных наибольших или возможных наименьших механических характеристик материалов элементов конструкций ТС всегда дает возможность получить технически возможные крайние параметры удара, что дает возможность получить категоричные выводы о параметрах движения автомобилей в момент их столкновения. Отметим, что достоверность МКЭ-модели удара признается и разработчиками инженерных моделей, и применяется ими как в экспертной практике, так и для проверки собственных упрощенных инженерных моделей [Day T.D., York A.R. Method for simulating collisions. // United States Patent №6195625].
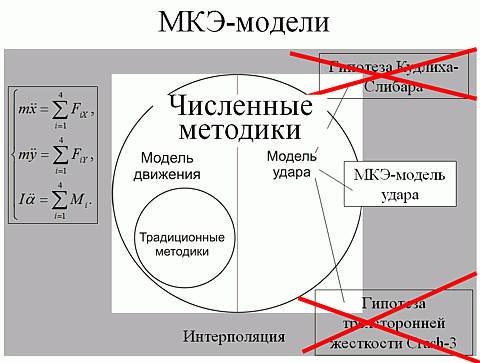Допустимость и объективность численной МКЭ-модели удара обусловлена тем, что модель строится на основе феноменологических исследований простейших ее составляющих – конечных элементов, – область определения воздействий на которые является полной и ограничивается только их разрушением. Описание конечных элементов методами механики деформируемого твердого тела не накладывает никаких ограничений на последовательность приложения воздействий в пространстве или времени, что делает МКЭ-модель удара интерполяционной и лишенной самой возможности экстраполяции за пределы области определения возможных воздействий при любом напряженно-деформированном состоянии. Замечательные свойства МКЭ: 1) Сходимость метода – метод имеет собственную возможность оценки погрешности решения задачи. 2) При заданных граничных условиях будет найдено решение, соответствующее минимуму расхода энергии. 3)Неполнота модели ТС гарантирует получение возможных наименьших затрат энергии. 4) Из-за использования упруго-идеальнопластической модели материала результат расчета не зависит от последовательности деформирования.
Таким образом, классификация математических моделей ДТП с точки зрения их интерполяционности выглядит следующим образом:
- Традиционные модели – интерполяционные, результат категоричный;
- Инженерные модели – экстраполяционные, результат вероятный;
- Численные модели – интерполяционные, результат категоричный.
Исторически сложилось так, что Российская судебная экспертиза не применяла и не применяет инженерные модели в практике судебных экспертных исследований. Однако бурное развитие мощности доступной вычислительной техники дает возможность перешагнуть этот этап развития и сразу перейти к использованию более наукоёмких, но допустимых в судебном процессе численных математических моделей удара на основе методов вычислительной механики.
Рейтинг публикации:
«
Уважаемый Владимир Николаевич, для юристов-практиков, наибольшее значение имеют конечно категоричные выводы, основанные на численных (интерполяционных) методах исследования.
При случае, я буду непременно обращать внимание на методы, используемые экспертами при подготовке заключений, и вполне возможно, что Ваши доводы могут стать основанием для назначения повторной экспертизы.
Во всяком случае, применяемые Вами методы визуализации, внушают больше доверия, чем куцие схемы, обычно встречающиеся в традиционных экспертных заключениях.
Очень серьезное исследование!(Y)(Y)(Y)
Вот уж точно говорят: «Век живи, век учись!» Спасибо за науку! (Y)
Возвращаемся к старым спорам :) Метод Владимира Николаевича — хорош, нет слов! Но откуда должна браться сама модель исследуемого ТС? Пока, насколько я знаю (может быть — уже не всё знаю?), модель СОЗДАЁТСЯ почти для каждого конкретного исследования, если только такой же автомобиль не исследовался раньше :( То есть, ко всем возможным методологическим неточностям (ошибкам) добавляются субъективные ошибки автора модели: из-за того, что он неверно определил толщины металла; из-за того, что он неверно определил марку стали; из-за того, что он ошибся несколько раз в линейных размерах и т.д. и т.п. Это я не упомянул процесс фиксации объёмных следов в зоне (зонах) следового контакта и зонах вызванных деформаций — там ошибок наберётся немеряно. Как быть? Как автор методики полагает решить эти вопросы? Или они решены?
Решены, но об этом позже. Я покажу примеры.:)
А откуда Вы взяли, что для МКЭ расчета «нужна модель исследуемого ТС»? Я где про это написал? А кто «автор модели ТС», если Вы — то Вы и отвечаете за точность, если я — где эта модель ТС? Вы о чем, Игорь Юрьевич? Абстрактно ни о чем, или про конкретный расчет?
Любая модель, в том числе в автотехнической экспертизе, создается по исходным данным органа, назначившего исследование. Я вам авторитетно разъясняю, что эксперт не вправе сам собирать доказательства. Запишите в себе в блокнот!
PS. Это я к тому, что нет гарантии, что автоэксперт Коненков не ошибется, нажав не на ту клавишу, при расчете остановочного пути. Или что его калькулятор не врет в седьмом разряде из-за заводского дефекта. А причем тут метод-то? Методика виновата? И о каких «возможных методологических неточностях (ошибках)» Вы пишите — давайте конкретно!
А «процесс фиксации объёмных следов в зоне (зонах) следового контакта » — это, если не ошибаюсь, трасология? Сообщаю, что и гинекологию я тоже не провожу.
Владимир Николаевич! Не вмешиваюсь в Ваш теоретический спор с Игорем Юрьевичем, но считаю что в автотехнической экспертизе (в общем ее понимании) нельзя делать выводы и анализ ТОЛЬКО по тем данным которые предоставляет орган, назначивший экспертизу. Все данные эксперт получает в результате осмотра транспортного средства, дорожного покрытия и других объектов экспертизы. В данном случае норма закона о запрете эксперта самостоятельно собирать информацию не работает и не будет работать. Если учитывать эту норму, то вопрос по определению восстановительной стоимости автомобиля должен звучать так «Какова восст. стоим. автомобиля на момент ДТП, которого повреждено: крыло, бампер, решетка радиатора (и перечисляем все детали автомобиля)?» ПРИ ответе эксперт НЕ ДОЛЖЕН включать детали, которые отсутствуют в вопросе. Согласитесь ПОЛНАЯ ЗАГРУЗКА ДЛЯ ЖЕНЩИН СУДЕЙ И АДВОКАТОВ.
И еще Владимир Николаевич — укажите примерный срок в днях на проведение переписки с органом, назначившим экспертизу, для предоставления необходимых Вам данных?
Дмитрий Геннадьевич, я это и имел в виду, осмотр. Осмотр проводит эксперт, он же измеряет то, что ему необходимо. И если трасолог занимается «процессом фиксации объёмных следов в зоне (зонах) следового контакта и зонах вызванных деформаций» — словесным описанием, для прочниста важенее данные: исходные размеры и форма, конечные размеры и форма в мм, см и т.д. — измерения. И ошибки измерения — это ошибки эксперта, а не метода расчета. Это те же самые ошибки, которые допускают и гайцы, составляя схему ДТП.
Реплика же Коненкова — следствие легенд, которые ходят по экспертному сообществу. Никто же умные журналы не читает — все пользуются слухами. :)
Срок переписки с органом — минимальный при наличии электронной почты и мобильной связи. Бывает, что в течении часа все решается.
Владимир Николаевич все правильно «ошибки измерения — это ошибки эксперта, а не метода расчета». Единственная «проблема» данного метода — отсутствие сформированной базы данных физических параметров деталей автомобиля. ЕЕ отсутствие заставляет только отдельных экспертов которые заинтересованы в объективном выводе применять «нетрадиционные» (для сознания большей массы специалистов)методы. И вторая проблема — недостаток времени для производства полномасштабных исследований. В соотношении цена-качество на современном этапе первую роль играет цена. Стороны не всегда готовы платить большие деньги за экспертизу (тем более зная о истине). Своих экспертов автотехников не могу заставить расширить доказательность выводов.
Дмитрий Геннадьевич, не торопитесь кресты и метки ставить, дождитесь публикаций конкретных экспертных исследований. Не так страшен метод, как его малюют.
Что такое «база данных физических параметров деталей автомобиля» я с трудом догадываюсь, и сомневаюсь в ее необходимости при наличии современных средств измерений. :)
А вот проблема — недостаток времени для производства полномасштабных исследований — это действительно проблема негосударственной экспертизы, которая ее и погубит. Я пытался донести мысль о том, что только на базе собственных исследований, с привлечением ученых крупные западные экспертные центры вырвались вперед и остались на рынке. Но, увы. Вместо этого идут бодрые рапорты о еженедельных научных конференциях (giggle) ....
Дело пойдет вперед, если зксперт (любой, и юрист тоже) убъет в себе ответчика за всю мировую науку. «Это — науке не известно, это — неправильно, потому что ...» — вот кредо экспертов. А наука смеется, не созрели вы, ребята!
Дмитрий Геннадьевич! Видимо, вы и эксперт такой самостоятельный, все доказательства соберу сам, проявлю заинтересованности по обвинению виновного, назначенного следователем, сам помогу составить приговор.
Ваше: «Нельзя делать выводы и анализ только по тем данным, которые предоставляет орган, назначивший экспертизу», граничит с преступлением, а попадись Вы мне в процесс, Вы бы, как эксперты Пермской ЛСЭ МЮ РФ, отказались бы от дачи показаний даже под страхом быть привлеченным к уголовной ответственности.
Специально для Вас: Следователь направляет материалы, необходимые для ее производства /ч.1 ст. 199 УПК РФ/, следователь в постановлении указывает какие материалы, предоставляются в распоряжение эксперта /п.4 ч.1 ст. 195 УПК РФ/. Эксперт вправе возвратить без исполнения постановление, если представленных материалов недостаточно для производства судебной экспертизы или он считает, что не обладает достаточными знаниями для ее производства /ч.5 ст. 199 УПК РФ/
А Ваше высказывание: «ПОЛНАЯ ЗАГРУЗКА ДЛЯ ЖЕНЩИН СУДЕЙ И АДВОКАТОВ» я понял как попытку самоутвердиться как эксперт хотя бы здесь.
Полагаю, что во внимание принимаются только новые автомобили. А как быть с гнилыми (ржавыми) либо восстановленными после ДТП автомобилями?
Где вы берете исходные данные прочности узлов и агрегатов транспортных средств при проведении своих расчетов? Такие данные являются сугубо частной собственностью производящей компании. Каждый производитель скрывает эту информацию от публичного доступа по причине конкуренции и шпионажа. У вас другие источники? Предоставьте и мне такую интересную информацию.
Не нужно заниматься популизмом. Доцентом вы стали, а додолларом сможете?
Совет. Полагайте что-нибудь в своей деятельности. Не отвечайте за производителей, они Вас не уполномочили. Производитель скрывает технологию получения свойств, но сами свойства он скрыть не может, он их даже рекламирует.
А в технике ничего не полагается, все определяется.
Комментаторами моя точка зрения, моя реплика, кажется понята, но понята ли она топикстартером? Поясняю: насколько я понимаю МЕТОДИКУ, осознавая при этом, что мои политехнические познания в сопромате (вкупе с методом конечных элементов) и в материаловедении весьма скудны по сравнению с познаниями Владимира Николаевича, чтобы исследовать затраты энергии на деформацию детали, следует создать модель детали. Точность определённых затрат энергии будет тем выше, чем точнее смоделирована сама деталь и фактически произошедшее с нею в результате механического воздействия (воздействий). Или я не понял чего-то?
К слову: где кончается «исследование» и начинается запретное «собирание доказательств» в области инженерно-технических экспертих никому не понятно. Грань — весьма зыбкая. Отболтать, ох, многое можно!
Игорь Юрьевич, чтобы исследовать затраты энергии на деформацию детали, следует создать модель детали. Точность определённых затрат энергии будет тем выше, чем точнее смоделирована сама деталь и фактически произошедшее с нею в результате механического воздействия (воздействий)да, конечно, до определенного предела. Но заметьте, сейчас Вы пишите о детали (одна, две, десять), а не об автомобиле в целом. А раньше Вы написали
откуда должна браться сама модель исследуемого ТС?Какая точность небходима для расчета деформации двери — один микрон, один миллиметр? :)
Расчетчик всегда может выполнить расчет так, чтобы расчетные затраты энергии были гарантированно меньше фактических или больше. Это его исскуство. При этом метод расчета снова не при чем, это же как не при чем таблица умножения, если ошибается расчетчик.
Так что голое теоретизирование о незнакомой методике далеко от практики ее применения.
Автомобиль состоит из деталей (и сборочных единиц). Оставим «искусство», займёмся наукой, которую среди нас Вы-то как раз и представляете — остальные (и я :-( ) — просто ремесленники :-( Из Ваших ответов я понимаю, что базы (библиотеки) кузовов ТС так и не создано? С материалами, толщинами и особенностями конструкции в смысле, например, наличия усилителей внутри двери :-( И не нужна Вам такая база? А последователям, буде запатентованный МЕТОД захочется внедрить пошире?
Лично мне — не нужна. Я сам умею измерять, да и средств хватает купить приборы для геометрических измерений и измерений свойств. Про последователей — читайте закон 73. Обязанности их начальников — обеспечить (giggle). Кто у вас в Гарборе начальник? Имеется ли оборудование?
Цитата с сайта:
Наши специалисты… действительными членами партнёрства «Палата Судебных Экспертов». Это позволяет ООО «ГАРБОР» регулярно проводить ...А я думал что проводить… позволяет наличине современного оборудования ...;(
Уели :) Фантиками попрекаете :-( Начальник — я. Приборы — дорогие — не по средствам малому предприятию, да и не каждый день нужны (очевидно, у Вас с этим — полный ажур). Под серьёзный проект, положим, можно взять в аренду сканирующий дальномер, но ПО к нему нету :-( Вот поэтому, в случае назначения подходящей экспертизы я просто буду ходатайствовать перед судом о включении в комиссию эксперта сторонней организации — Вас, Владимир Николаевич. Однако мы утомили читателей переходом на личности. Для всех: ИМХО, следует иметь (создать?) библиотеку кузовов ТС, в частности, для повторяемости и проверяемости результатов применения Вашей патентованной методики.
Резюмируем: в судебном процессе математические модели допустимы, методы уважаемого Владимира Николаевича — применимы, но только, увы, пока он колдует сам, демонстрирует «искусство» :) Как бы из этого чуда сделать инструмент? Как бы методы сделать «общепринятыми»? Вот в чём вопросы. Риторические, наверное…
И я резюмирую.
Аханьем и оханьем «общепринятыми» ничего не сделаешь, кадры не выучишь, базы данных не создашь. То, что нашему государству научно-технический прогресс не нужен, понятно. А где многочисленные негосударственные экспертные организации, которые прогресс сделает конкурентоспособными? Они спят и мечтают, что однажды «по щучьему велению» ... (dance)
Без государственной сиськи — никак :( А может Вам в Сколково постучаться? Инновации, типа, хочу поучаствовать в распиле средств :( Готов поделиться, типа :P
Если серьёзно, заметными (возможно — достаточными) средствами обладают только такие монстры как АНО «Центр Судебных Экспертиз» г-на Костюченко. К нему обратиться — попробуйте или к таким же наподобие. Остальные — выживают просто, не до инвестиций :-(
А вообще, существует ли какой-то «бизнес-план» по доработке МЕТОДИКИ до товарного вида? Чтобы купить продукт и пользоваться, как Аудатексом, как Каратом? Имеется ли представление, что и сколько для этого надо? Кроме (ИМХО!) сведений от производителей ТС?
Такие расчеты делали в 2008г. Речь шла о создании достаточно дешевого софта по МКЭ, так как возможности существующего на 80% для ДТП не нужны. Прогу типа Карата я для себя сам написал, можно, конечно и нужно, графику доработать. Но работает не хуже, и есть функции, которых нет в Карате.
Только на АНО ЦСЭ, видимо ставить не надо. Это я из принципа не класть яйца в одну корзину. А если несколько выживающих объединятся для решения этой задачи, то можно потянуть. Но желания-то и нет. Живете одним днем все.
Обобщены и приговорены (giggle) У Вас желание — есть? Пока ещё, видимо, есть :) У меня желание есть. Многие подпишутся, что есть. А как объединиться предлагаете? Скинуться? О каких суммах речь? (wasntme)
Я подумаю. (handshake)
Вам бы, Владимир Николаевич, софт создать дешевле некуда! Чтоб значит вместо судьи, прокурора и адвоката — хорошо обученные операторы компьютерного ввода. Прокурор забивает на перфокарту доказательства, адвокат забивает доказательства того, почему эти доказательства не доказательства, судья проверяет, чтоб не мухлевали и расписывается. Все забивается в компутер и он выдает: виновен! Срок — 2234 дня лишения свободы. Или — невиновен! Компьютеру следственного комитета высланы указания а) привлечь следователя к уголовной ответсвенности за фальсификацию, б) удержать у следователя 25% зарплаты за неумение процессуально закреплять доказательства
Софт создать — не проблема. Проблема в том, что забьёт прокурор. Если как «волшебник Чуров», то никакой софт не справится. (giggle)
Так вторая инстанция пусть будет человеческая, но далеко. Может и набавить типа
Не может! Может только убавить или оставить как есть.
Подсудимому или убавить или оставить. Это — конституционно. А прокурору можно и добавить:)
Уважаемый Николай Владимирович, Что Вы скажите о выказывании: «В итоге Горюнов вместе с юристом подал иск в Высокогорский районный суд. На заседаниях удалось доказать, что так как работа мобильного фоторадара основана на эффекте Доплера (скорость транспортного средства измеряется по изменению частоты отраженного сигнала радиолокатора), на него оказывают влияние свойства среды, в которой распространяются излучаемые электромагнитные волны. Поэтому комплекс должен устанавливаться в соответствии с инструкцией — на высоте не ниже полуметра и не выше двух метров»? На https://auto.mail.ru/...d_s_pomoshchyu_zakonov_fiziki/ .
Уважаемый Александр Валериевич, все правильно. Это не первый случай, когда гайцы устанавливают радары не по инстсрукции.