Найти юриста / адвоката / эксперта
Как часто в заключениях экспертов по ДТП вам приходилось видеть некие мыслепододобные рассуждения, закачивающиеся утверждением «наиболее вероятно …»? А почему не просто «вероятно»? И что это, обычный оборот речи или вывод, подкрепленный теорией вероятности?
Откуда эксперт знает, что «вероятно» или даже «наиболее вероятно», а что «менее вероятно»?
Адвокаты, сталкиваясь с такой фразой, конечно, пытаются ее опровергнуть, но, увы, путем того же пустого словопрения. Однако, как будет показано ниже, эти термины имеют вполне детерминированные значения.
В самом деле, мощности даже самого скромного персонального компьютера достаточно, чтобы оценить практически все возможные комбинации набора технических параметров, описывающих ДТП, и изменяющихся, с учетом погрешности их определения, от А до Я. А после определить уровень доверия тому или иному результату, или его вероятность. Для этого идеально подходит метод Монте-Карло.
Вероятность – степень (относительная мера, количественная оценка) возможности наступления некоторого события. Когда основания для того, чтобы какое-нибудь возможное событие произошло в действительности, перевешивают противоположные основания, то это событие называют вероятным, в противном случае – маловероятным или невероятным. Перевес положительных оснований над отрицательными, и наоборот, может быть в различной степени, вследствие чего вероятность (и невероятность) бывает большей или меньшей.
Например, вероятность того, что, например, при бросании кубика выпадет число «5», равна 1/6, так как у кубика шесть граней, и выпадение любого числа от «1» до «6» равновероятно. А вот вероятность сочетания двух событий, что бри бросании двух кубиков на них одновременно выпадет число «5», уже равна 1/36, так как всего есть 36 комбинаций выпавших чисел на двух кубиках.
Наступление какого-то события – дело случая. А вот распределение вероятностей наступления события – это закон, описывающий область значений случайной величины и вероятности их принятия. Наиболее известное распределение – это нормальное распределение, также называемое распределением Гаусса. Это – распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности
Выглядит немного пугающе, но сейчас разберемся. В функции плотности нормального распределения присутствуют две математические константы: π – соотношение длины окружности и его диаметра, равно примерно 3.14, е – основание натурального логарифма, равно примерно 2.718, и два параметра, которые задают форму конкретной кривой: m – математическое ожидание, σ2 – дисперсия (мера разброса данной случайной величины, то есть её отклонения от математического ожидания.), ну и сама случайная величина x, для которой высчитывается значение функции, т.е. плотность вероятности.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности, что хорошо видно на картинке. А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса сконцентрирована у центра. Если же у данных большой разброс, то они «размажутся» по широкому диапазону.
Закону нормального распределения подчиняется множество величин. Например, рост взрослых людей, или длина взрослых крокодилов одной породы. Другие величины, в том числе, описывающие ДТП, могут подчиняться закону равномерного распределения, когда вместо колокольной кривой на графике плотности вероятности будет прямая, параллельная оси абсцисс.
Сцепление шин с сухим асфальтом
При реконструкции обстоятельств ДТП автоэксперты, как правило, исходя их данных о дорожном покрытии, выбирают по нормативным таблицам значение коэффициента сцепления шин с дорогой, или, проще, коэффициента трения. Так, например, нормативное значение коэффициента сцепления в России составляет 0.7-0.8 для сухого эксплуатируемого асфальта и 0.6-0.7 для свежеуложенного.
Следовало бы ожидать, что широко используемые в судебной экспертизе таблицы коэффициентов сцепления были созданы путем проведения тщательно документированных испытаний на различных поверхностях и с различными шинами. Но это не так. Автомобили и их тормозные системы совершенствуются, а в России таблицы остаются прежними, как и в 60-х годах прошлого века, да и отчетов про те испытания уже не найти. Но если государственные судебно-экспертные учреждения не могут или не хотят предоставить обоснование, то можно ли рассматривать эти таблицы как неприкасаемый священный Талмуд?
В последние годы стало ясно, что взаимодействие шин и дорожного покрытия при торможении или заносе не соответствует простой, независящей от массы и скорости транспортного средства, модели трения, и точность табличных коэффициентов сцепления вызывает сомнение [1, 2]. Табличные значения для коэффициентов сцепления шин на асфальте и бетоне не согласуются с более поздними литературными данными [3]. Обзор этих данных в подавляющем большинстве случаев показывает, что значения коэффициентов сцепления являются слишком низкими для современных автомобилей, оснащенных современными шинами, и на современных дорогах.
Далее приводятся значения коэффициентов сцепления шин с сухим асфальтом для автомобилей, не оснащенных АБС. Так, по данным [4], среднее значение коэффициента сцепления составляет 0.72-0.78. По данным [5], значение коэффициента сцепления составляет 0.76 для текстурированного асфальтобетона. По данным [6], при испытании на занос на гладком участке значения коэффициента сцепления составили 0.78-0.80.
Авторы [7] использовали три различных «класса» доступных шин для легковых автомобилей и провели сотни испытаний. В среднем для всех их испытаний, на сухом асфальте коэффициент сцепления шин с дорогой был 0.828 ± 0.033, и подчинялся закону нормального распределения Гаусса, как показано на рисунке ниже.
Оценивая представленные значения коэффициентов сцепления шин с сухим асфальтом из нескольких различных источников с использованием различных транспортных средств, водителей, поверхностей, измерительных инструментов и методов анализа, среднее значение составляет 0.76 ± 0.06.
Учитывая, что среднее значение среднее значение коэффициента сцепления шин с сухим асфальтом составляет 0.76 ± 0.06, в 95% всех случаев можно ожидать значения между 0.64 и 0.88. На рисунке ниже показано кумулятивное распределение вероятностей для этих статистических данных. Если исключить наличие посторонних материалов на дорожном покрытии (битум, песок и т.п.), значение коэффициента сцепления 0.6 довольно маловероятно, так как реализуется менее чем в 4-х случаях из 1000, или иначе говоря, реже, чем в более 99.61% всех случаев. Даже значение коэффициента сцепления 0.7 также маловероятно, так как реализуется меньше чем в 84.1% всех случаев.
Название и содержание этого раздела совпадет с названием и содержанием замечательной работы польского автоэксперта Войцеха Вача из Института судебной экспертизы в Кракове.
Важной проблемой, свойственной реконструкции обстоятельств ДТП, является относительно скудный набор данных, которые были собраны на месте ДТП, и необходимость введения многих параметров с широким диапазоном их возможных значений, что повышает неопределенность результатов расчета. Однако метод Монте-Карло позволяет представить результат в виде функции плотности вероятности для расчетных параметров.
Иными словами, на практике мы имеем ряд параметров, которые в разумных пределах могут отклоняться от принятого экспертом значения, а статистическое распределение значений этих параметров подчиняется либо закону нормального распределения Гаусса, либо закону равномерного распределения. Тогда требуется произвести несколько десятков тысяч расчетов с разным сочетанием значений этих параметров, чтобы установить наиболее вероятный вариант развития событий в ДТП. Или, проще говоря, поиграть с этими параметрами в рулетку.
Пример 1. Скорость перед началом торможения
Рассмотрим простой пример, когда метод Монте-Карло используется для расчета скорости транспортного средства. Известна длина следа торможения 20 м. Среднее значение коэффициента сцепления принято 0.8, в соответствии с нормативными таблицами. Тогда, без учета времени нарастания замедления, простейшим расчетом получаем ответ – 17.7 м/с.
Однако, погрешность в измерении длины следа составляет ±0.9 м (неважно, как это установлено), погрешность значения коэффициента сцепления составляет ±0.06 (см. выше).
Кажется, что здесь проблемы нет – делаем два расчета. Один с минимальными значениями параметров, второй с максимальными. Получаем диапазон 16.7-18.8 м/с. Или скорость была 17.7±1.1 м/с, где 1.1 м/с – наибольшее возможное отклонение скорости. Или скорость была 17.7±0.78 м/с, где 0.78 м/с – среднеквадратичное отклонение скорости.
Расчет по той же простейшей формуле определения скорости был проведен методом Монте-Карло 20 000 раз для однородных распределений параметров длины тормозного следа и коэффициента сцепления. Распределение результатов в виде колоколообразной кривой показано синим цветом на графике на рисунке выше.
Затем, аналогичное моделирование выполнено с параметрами, подчиняющимися нормальному распределению, для значений дисперсии для длины тормозного пути 0.9/3=0.3 м и коэффициента сцепления 0.06/3=0.02 в соответствии с правилом трех сигм. Распределение результатов в виде колоколообразной кривой показано черным цветом на графике на рисунке выше. Там же черной штриховой линией показано теоретическое нормальное распределение, и видно, что оно близко к полученному методом Монте-Карло.
Как видно из рисунка выше, наиболее вероятный диапазон скорости в пределах дисперсии от максимума на графике – это 17.7±0.36 м/с. Конечно, на практике такие расчеты скорости не нужны. Они приведены как для иллюстрации метода Монте-Карло, так и для иллюстрации конкретного наполнения содержанием слов «наиболее вероятно» в заключениях экспертов. А это уже весьма полезно адвокатам.
Другими словами, эксперт «за свой базар» должен ответить – написал, что что-то «наиболее вероятно», покажи расчеты этой вероятности. Нет расчетов – значит выдумал.
Пример 2. Столкновение двух автомобилей
Для инсценированного ДТП, схема которого была показана выше, при расчетах методом Монте-Карло учитывались отклонения коэффициентов сцепления шин автомобилей с дорогой, масс автомобилей и их моментов инерции, углов между их продольными осями в момент столкновения и между векторами скоростей их центров тяжести в момент разделения автомобилей.
В результате моделирования методом Монте-Карло, были получены функции плотности вероятности скоростей, которые показаны на рисунке выше. Ожидаемые (номинальные) значения скоростей в момент столкновения v1=86.6 км/ч и v2=1.2 км/ч. Для сравнения, истинные значения этих скоростей v1=87.7 км/ч и v2= 0 км/ч.
Представление результатов в виде графиков плотности вероятности скоростей отдельно для каждого автомобиля влечет за собой риск селективного и некорректного выбора любого из значений в суде, например, чтобы убедить суд в правоте своей позиции в ходе судебного разбирательства. Таким образом, лучшее решение с формальной точки зрения является представление результата в виде трехмерного графика функции плотности вероятности, где плотность вероятности зависит от двух параметров – скоростей каждого из автомобилей, как показано на рисунке ниже.
Пример 3. Определение места столкновения
Обратимся к интригующей проблеме расчетного определения места столкновения двух транспортных средств в случае, если какие-либо следы, которые однозначно указывают на местоположение этого места, не были обнаружены на поверхности дороги. Для этого используем предыдущий пример столкновения двух автомобилей, но теперь этот случай будет рассмотрен, как если бы были известны только деформации транспортных средств, конечные позиции транспортных средств, а также тот факт, что транспортные средства были перпендикулярны друг к другу в момент удара.
То есть, вместо учета возможного разброса углов между продольными осями автомобилей в момент столкновения в этом расчете предполагалась погрешность в положении точки столкновения по координатам x и y.
Учитывались только те значения плотности вероятности, которые обеспечивали положительное значение скорости разделения автомобилей, и которые обеспечивали попадание автомобилей в их конечное положение.
На рисунке выше справа показан трехмерный график плотности вероятности, построенный на координатах x и y. Его проекция на плоскость показана на схеме слева. Видно, что расчетная точка столкновения С определена с погрешностью 0.39 м от истинной точки столкновения С’.
То есть результат очень хороший, и в любом случае проекцию на дорогу верхней трети графика плотности вероятности справа на рисунке, куда входит и истинная точка столкновения, можно научно обоснованно характеризовать как наиболее вероятное место столкновения. И это будут не пустые слова.
Приведенные примеры показали высокую эффективность метода Монте-Карло при реконструкции обстоятельств ДТП. Применение метода Монте-Карло легитимно для российской автотехнической экспертизы, так как модуль подобного анализа содержится в рекомендованной МЮ РФ программе моделирования ДТП PC-Crash.
В свете математической теории вероятности и ее физического прикладного применения к анализу ДТП выяснилось, что термины «более вероятно» или «менее вероятно», широко использующиеся в российской экспертной практике, как правило, не являются результатом научного анализа, в связи с чем их можно трактовать как попытку ввести суды в заблуждение с целью доказать свою субъективную точку зрения.
Отрадно, что этот обзор применения метода Монте-Карло написан автором не только на основе результатов американских научных публикаций, но и статьи польского автоэксперта. Невольное сравнение квалификации судебного эксперта соседней с нами страны с тем, что мы имеет в государственной экспертизе у себя, вызывает, по меньшей мере, чувство досады.
Юридическое осмысление приведенной информации, ее широкое обсуждение, несомненно, будет полезным, как для автора, так и для самих юристов, так как в их арсенале появляется новый мощный инструмент защиты.
2. Navin, F., Drag sled and automobile skidding, an analytical relationship, by University of British Columbia President, SYNECTICS RSR Corp. Vancouver, USA SPECIAL PROBLEMS 2009 Orlando, Florida, April 2009.
3. Jernigan, Jack D., Metem F. Kodaman. An Investigation of the Utility and Accuracy of the Table of Speed and Stopping Distances Specified in the Code of Virginia. Virginia Transportation Research Council, Charlottesville VA. Report VTRC 01-R13. May 2001.
4. Bellion, Peter. Project Y.A.M. (Yaw Analysis Methodology) vehicle testing and findings. SAE Paper 970955. 1997.
5. Brown, E.C., P.D.Cenek. Tyre Road Friction Coefficients for Crash Recon: Overview of New Zealand Experience. ASPACI «Fact or Friction» Conference. Adalaide Australia. March 2002.
6. National Transportation Safety Board. Passenger Vehicle Median Crossover and Head-On Collision With Another Passenger Vehicle, Linden, New Jersey, May 1, 2003. Highway Accident Report NTSB/HAR-06/02. Washington, DC. Adopted February 7, 2006.
7. Goudie, D.W., J.J.Bowler, C.A.Brown, B.E.Heinrichs. Tire Friction During Locked Wheel Braking. SAE Paper 2000-01-1314. 2000.
Откуда эксперт знает, что «вероятно» или даже «наиболее вероятно», а что «менее вероятно»?
Адвокаты, сталкиваясь с такой фразой, конечно, пытаются ее опровергнуть, но, увы, путем того же пустого словопрения. Однако, как будет показано ниже, эти термины имеют вполне детерминированные значения.
В самом деле, мощности даже самого скромного персонального компьютера достаточно, чтобы оценить практически все возможные комбинации набора технических параметров, описывающих ДТП, и изменяющихся, с учетом погрешности их определения, от А до Я. А после определить уровень доверия тому или иному результату, или его вероятность. Для этого идеально подходит метод Монте-Карло.
Вероятность – степень (относительная мера, количественная оценка) возможности наступления некоторого события. Когда основания для того, чтобы какое-нибудь возможное событие произошло в действительности, перевешивают противоположные основания, то это событие называют вероятным, в противном случае – маловероятным или невероятным. Перевес положительных оснований над отрицательными, и наоборот, может быть в различной степени, вследствие чего вероятность (и невероятность) бывает большей или меньшей.
Например, вероятность того, что, например, при бросании кубика выпадет число «5», равна 1/6, так как у кубика шесть граней, и выпадение любого числа от «1» до «6» равновероятно. А вот вероятность сочетания двух событий, что бри бросании двух кубиков на них одновременно выпадет число «5», уже равна 1/36, так как всего есть 36 комбинаций выпавших чисел на двух кубиках.
Наступление какого-то события – дело случая. А вот распределение вероятностей наступления события – это закон, описывающий область значений случайной величины и вероятности их принятия. Наиболее известное распределение – это нормальное распределение, также называемое распределением Гаусса. Это – распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности
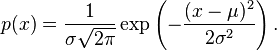
Выглядит немного пугающе, но сейчас разберемся. В функции плотности нормального распределения присутствуют две математические константы: π – соотношение длины окружности и его диаметра, равно примерно 3.14, е – основание натурального логарифма, равно примерно 2.718, и два параметра, которые задают форму конкретной кривой: m – математическое ожидание, σ2 – дисперсия (мера разброса данной случайной величины, то есть её отклонения от математического ожидания.), ну и сама случайная величина x, для которой высчитывается значение функции, т.е. плотность вероятности.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности, что хорошо видно на картинке. А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса сконцентрирована у центра. Если же у данных большой разброс, то они «размажутся» по широкому диапазону.
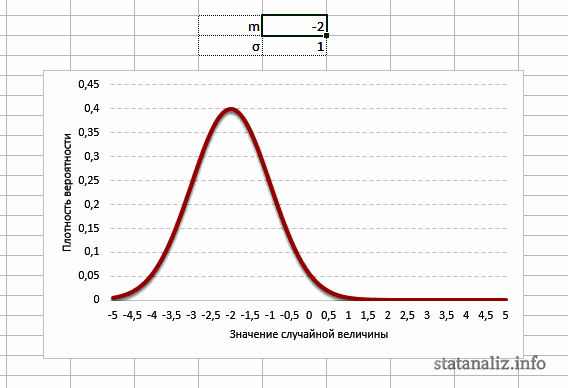
Закону нормального распределения подчиняется множество величин. Например, рост взрослых людей, или длина взрослых крокодилов одной породы. Другие величины, в том числе, описывающие ДТП, могут подчиняться закону равномерного распределения, когда вместо колокольной кривой на графике плотности вероятности будет прямая, параллельная оси абсцисс.
Сцепление шин с сухим асфальтом
При реконструкции обстоятельств ДТП автоэксперты, как правило, исходя их данных о дорожном покрытии, выбирают по нормативным таблицам значение коэффициента сцепления шин с дорогой, или, проще, коэффициента трения. Так, например, нормативное значение коэффициента сцепления в России составляет 0.7-0.8 для сухого эксплуатируемого асфальта и 0.6-0.7 для свежеуложенного.
Следовало бы ожидать, что широко используемые в судебной экспертизе таблицы коэффициентов сцепления были созданы путем проведения тщательно документированных испытаний на различных поверхностях и с различными шинами. Но это не так. Автомобили и их тормозные системы совершенствуются, а в России таблицы остаются прежними, как и в 60-х годах прошлого века, да и отчетов про те испытания уже не найти. Но если государственные судебно-экспертные учреждения не могут или не хотят предоставить обоснование, то можно ли рассматривать эти таблицы как неприкасаемый священный Талмуд?
В последние годы стало ясно, что взаимодействие шин и дорожного покрытия при торможении или заносе не соответствует простой, независящей от массы и скорости транспортного средства, модели трения, и точность табличных коэффициентов сцепления вызывает сомнение [1, 2]. Табличные значения для коэффициентов сцепления шин на асфальте и бетоне не согласуются с более поздними литературными данными [3]. Обзор этих данных в подавляющем большинстве случаев показывает, что значения коэффициентов сцепления являются слишком низкими для современных автомобилей, оснащенных современными шинами, и на современных дорогах.
Далее приводятся значения коэффициентов сцепления шин с сухим асфальтом для автомобилей, не оснащенных АБС. Так, по данным [4], среднее значение коэффициента сцепления составляет 0.72-0.78. По данным [5], значение коэффициента сцепления составляет 0.76 для текстурированного асфальтобетона. По данным [6], при испытании на занос на гладком участке значения коэффициента сцепления составили 0.78-0.80.
Авторы [7] использовали три различных «класса» доступных шин для легковых автомобилей и провели сотни испытаний. В среднем для всех их испытаний, на сухом асфальте коэффициент сцепления шин с дорогой был 0.828 ± 0.033, и подчинялся закону нормального распределения Гаусса, как показано на рисунке ниже.
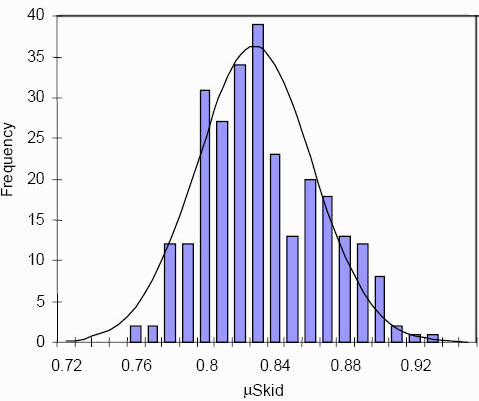
Оценивая представленные значения коэффициентов сцепления шин с сухим асфальтом из нескольких различных источников с использованием различных транспортных средств, водителей, поверхностей, измерительных инструментов и методов анализа, среднее значение составляет 0.76 ± 0.06.
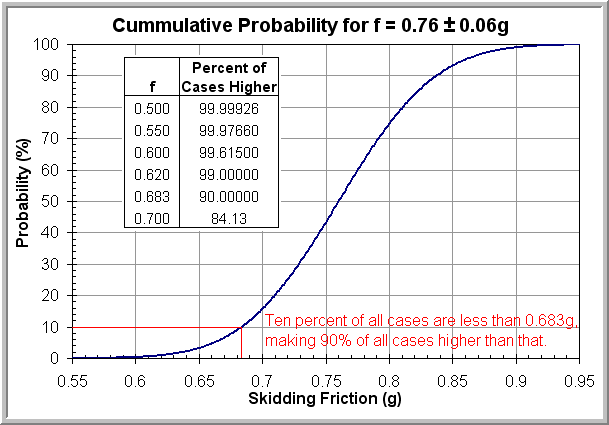
Учитывая, что среднее значение среднее значение коэффициента сцепления шин с сухим асфальтом составляет 0.76 ± 0.06, в 95% всех случаев можно ожидать значения между 0.64 и 0.88. На рисунке ниже показано кумулятивное распределение вероятностей для этих статистических данных. Если исключить наличие посторонних материалов на дорожном покрытии (битум, песок и т.п.), значение коэффициента сцепления 0.6 довольно маловероятно, так как реализуется менее чем в 4-х случаях из 1000, или иначе говоря, реже, чем в более 99.61% всех случаев. Даже значение коэффициента сцепления 0.7 также маловероятно, так как реализуется меньше чем в 84.1% всех случаев.
Метод Монте-Карло против интерпретации расчетных результатов в анализе дорожно-транспортных происшествий
Название и содержание этого раздела совпадет с названием и содержанием замечательной работы польского автоэксперта Войцеха Вача из Института судебной экспертизы в Кракове.
Важной проблемой, свойственной реконструкции обстоятельств ДТП, является относительно скудный набор данных, которые были собраны на месте ДТП, и необходимость введения многих параметров с широким диапазоном их возможных значений, что повышает неопределенность результатов расчета. Однако метод Монте-Карло позволяет представить результат в виде функции плотности вероятности для расчетных параметров.
Иными словами, на практике мы имеем ряд параметров, которые в разумных пределах могут отклоняться от принятого экспертом значения, а статистическое распределение значений этих параметров подчиняется либо закону нормального распределения Гаусса, либо закону равномерного распределения. Тогда требуется произвести несколько десятков тысяч расчетов с разным сочетанием значений этих параметров, чтобы установить наиболее вероятный вариант развития событий в ДТП. Или, проще говоря, поиграть с этими параметрами в рулетку.
Пример 1. Скорость перед началом торможения
Рассмотрим простой пример, когда метод Монте-Карло используется для расчета скорости транспортного средства. Известна длина следа торможения 20 м. Среднее значение коэффициента сцепления принято 0.8, в соответствии с нормативными таблицами. Тогда, без учета времени нарастания замедления, простейшим расчетом получаем ответ – 17.7 м/с.
Однако, погрешность в измерении длины следа составляет ±0.9 м (неважно, как это установлено), погрешность значения коэффициента сцепления составляет ±0.06 (см. выше).
Кажется, что здесь проблемы нет – делаем два расчета. Один с минимальными значениями параметров, второй с максимальными. Получаем диапазон 16.7-18.8 м/с. Или скорость была 17.7±1.1 м/с, где 1.1 м/с – наибольшее возможное отклонение скорости. Или скорость была 17.7±0.78 м/с, где 0.78 м/с – среднеквадратичное отклонение скорости.
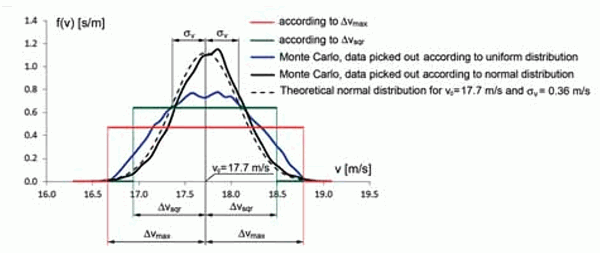
Расчет по той же простейшей формуле определения скорости был проведен методом Монте-Карло 20 000 раз для однородных распределений параметров длины тормозного следа и коэффициента сцепления. Распределение результатов в виде колоколообразной кривой показано синим цветом на графике на рисунке выше.
Затем, аналогичное моделирование выполнено с параметрами, подчиняющимися нормальному распределению, для значений дисперсии для длины тормозного пути 0.9/3=0.3 м и коэффициента сцепления 0.06/3=0.02 в соответствии с правилом трех сигм. Распределение результатов в виде колоколообразной кривой показано черным цветом на графике на рисунке выше. Там же черной штриховой линией показано теоретическое нормальное распределение, и видно, что оно близко к полученному методом Монте-Карло.
Как видно из рисунка выше, наиболее вероятный диапазон скорости в пределах дисперсии от максимума на графике – это 17.7±0.36 м/с. Конечно, на практике такие расчеты скорости не нужны. Они приведены как для иллюстрации метода Монте-Карло, так и для иллюстрации конкретного наполнения содержанием слов «наиболее вероятно» в заключениях экспертов. А это уже весьма полезно адвокатам.
Другими словами, эксперт «за свой базар» должен ответить – написал, что что-то «наиболее вероятно», покажи расчеты этой вероятности. Нет расчетов – значит выдумал.
Пример 2. Столкновение двух автомобилей
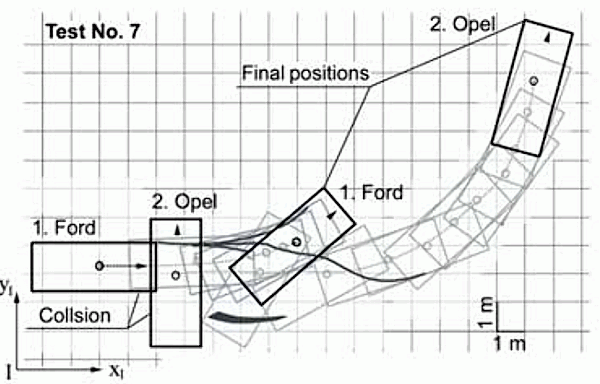
Для инсценированного ДТП, схема которого была показана выше, при расчетах методом Монте-Карло учитывались отклонения коэффициентов сцепления шин автомобилей с дорогой, масс автомобилей и их моментов инерции, углов между их продольными осями в момент столкновения и между векторами скоростей их центров тяжести в момент разделения автомобилей.
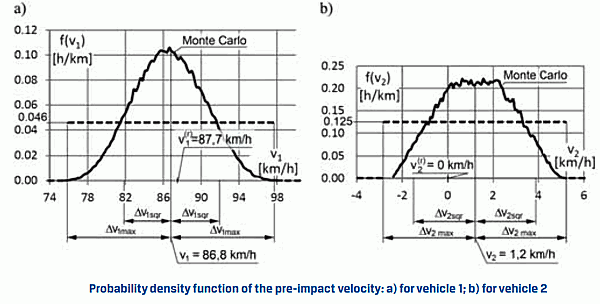
В результате моделирования методом Монте-Карло, были получены функции плотности вероятности скоростей, которые показаны на рисунке выше. Ожидаемые (номинальные) значения скоростей в момент столкновения v1=86.6 км/ч и v2=1.2 км/ч. Для сравнения, истинные значения этих скоростей v1=87.7 км/ч и v2= 0 км/ч.
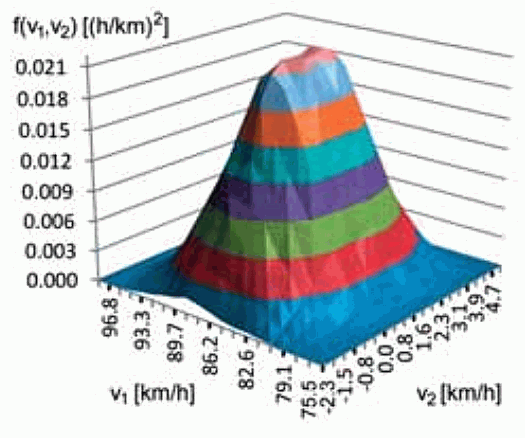
Представление результатов в виде графиков плотности вероятности скоростей отдельно для каждого автомобиля влечет за собой риск селективного и некорректного выбора любого из значений в суде, например, чтобы убедить суд в правоте своей позиции в ходе судебного разбирательства. Таким образом, лучшее решение с формальной точки зрения является представление результата в виде трехмерного графика функции плотности вероятности, где плотность вероятности зависит от двух параметров – скоростей каждого из автомобилей, как показано на рисунке ниже.
Пример 3. Определение места столкновения
Обратимся к интригующей проблеме расчетного определения места столкновения двух транспортных средств в случае, если какие-либо следы, которые однозначно указывают на местоположение этого места, не были обнаружены на поверхности дороги. Для этого используем предыдущий пример столкновения двух автомобилей, но теперь этот случай будет рассмотрен, как если бы были известны только деформации транспортных средств, конечные позиции транспортных средств, а также тот факт, что транспортные средства были перпендикулярны друг к другу в момент удара.
То есть, вместо учета возможного разброса углов между продольными осями автомобилей в момент столкновения в этом расчете предполагалась погрешность в положении точки столкновения по координатам x и y.
Учитывались только те значения плотности вероятности, которые обеспечивали положительное значение скорости разделения автомобилей, и которые обеспечивали попадание автомобилей в их конечное положение.
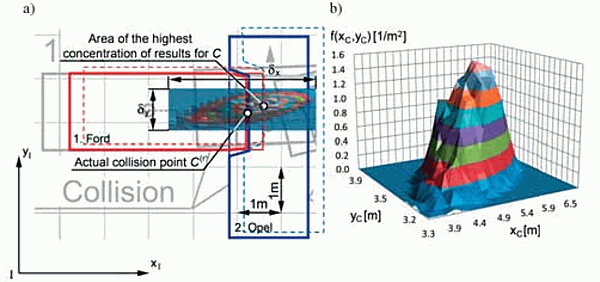
На рисунке выше справа показан трехмерный график плотности вероятности, построенный на координатах x и y. Его проекция на плоскость показана на схеме слева. Видно, что расчетная точка столкновения С определена с погрешностью 0.39 м от истинной точки столкновения С’.
То есть результат очень хороший, и в любом случае проекцию на дорогу верхней трети графика плотности вероятности справа на рисунке, куда входит и истинная точка столкновения, можно научно обоснованно характеризовать как наиболее вероятное место столкновения. И это будут не пустые слова.
Краткие итоги
Приведенные примеры показали высокую эффективность метода Монте-Карло при реконструкции обстоятельств ДТП. Применение метода Монте-Карло легитимно для российской автотехнической экспертизы, так как модуль подобного анализа содержится в рекомендованной МЮ РФ программе моделирования ДТП PC-Crash.
В свете математической теории вероятности и ее физического прикладного применения к анализу ДТП выяснилось, что термины «более вероятно» или «менее вероятно», широко использующиеся в российской экспертной практике, как правило, не являются результатом научного анализа, в связи с чем их можно трактовать как попытку ввести суды в заблуждение с целью доказать свою субъективную точку зрения.
Отрадно, что этот обзор применения метода Монте-Карло написан автором не только на основе результатов американских научных публикаций, но и статьи польского автоэксперта. Невольное сравнение квалификации судебного эксперта соседней с нами страны с тем, что мы имеет в государственной экспертизе у себя, вызывает, по меньшей мере, чувство досады.
Юридическое осмысление приведенной информации, ее широкое обсуждение, несомненно, будет полезным, как для автора, так и для самих юристов, так как в их арсенале появляется новый мощный инструмент защиты.
Литература:
1. Bartlett, W., Baxter, A., Livesay, E., Schmidt, B. et al., «Comparison of Drag-Sled and Skidding-Vehicle Drag Factors on Dry Roadways,» SAE Technical Paper 2006-01-1398, 2006, doi:10.4271/2006-01-1398.2. Navin, F., Drag sled and automobile skidding, an analytical relationship, by University of British Columbia President, SYNECTICS RSR Corp. Vancouver, USA SPECIAL PROBLEMS 2009 Orlando, Florida, April 2009.
3. Jernigan, Jack D., Metem F. Kodaman. An Investigation of the Utility and Accuracy of the Table of Speed and Stopping Distances Specified in the Code of Virginia. Virginia Transportation Research Council, Charlottesville VA. Report VTRC 01-R13. May 2001.
4. Bellion, Peter. Project Y.A.M. (Yaw Analysis Methodology) vehicle testing and findings. SAE Paper 970955. 1997.
5. Brown, E.C., P.D.Cenek. Tyre Road Friction Coefficients for Crash Recon: Overview of New Zealand Experience. ASPACI «Fact or Friction» Conference. Adalaide Australia. March 2002.
6. National Transportation Safety Board. Passenger Vehicle Median Crossover and Head-On Collision With Another Passenger Vehicle, Linden, New Jersey, May 1, 2003. Highway Accident Report NTSB/HAR-06/02. Washington, DC. Adopted February 7, 2006.
7. Goudie, D.W., J.J.Bowler, C.A.Brown, B.E.Heinrichs. Tire Friction During Locked Wheel Braking. SAE Paper 2000-01-1314. 2000.
Рейтинг публикации:
«
Уважаемый Владимир Николаевич, как всегда — отлично!
И сразу вопрос, может что и посоветуете
Мне в практической деятельности нередко приходится сталкиваться с формулировками судебно-медицинских экспертов, которые начинаются со слов: «наиболее вероятно, что данное повреждение образовалось в результате ....»
Разумеется, что никаких расчетов вероятности при этом не производятся
Я в таких случаях задаю встречный вопрос — а какая вероятность этого события в процентах?
В ответ, как правило, идет бессмысленное мычание.
А что Вы бы посоветовали в такой ситуации?
Уважаемый Эдуард Викторович, как видите, вероятность легко просчитывается. Надо выделить набор исходных параметров и определиться с их диапазоном значений. Ну, естественно, освоить азы программирования :)
Уважаемый Эдуард Викторович!
Я в восторге от всегда точных построений автора публикации.
Но до применения их в практике, и не только в судебно-медицинской, надо решить вопрос о соотношении понятий «вероятность» и «сомнения», «предположения».
Статья 14. Презумпция невиновности
1. Обвиняемый считается невиновным, пока его виновность в совершении преступления не будет доказана в предусмотренном настоящим Кодексом порядке и установлена вступившим в законную силу приговором суда.
2. Подозреваемый или обвиняемый не обязан доказывать свою невиновность. Бремя доказывания обвинения и опровержения доводов, приводимых в защиту подозреваемого или обвиняемого, лежит на стороне обвинения.
3. Все сомнения в виновности обвиняемого, которые не могут быть устранены в порядке, установленном настоящим Кодексом, толкуются в пользу обвиняемого.
4. Обвинительный приговор не может быть основан на предположениях.
Уважаемый Владимир Николаевич, а особенно интересно, когда эксперт пишет, что угол столкновения вероятнее всего столько-то градусов, но расчет не приводит! А когда их вызываю на допрос, то они почему то в отпуск уходят. Суды проглатывают это, типа нет оснований не доверять… печально! Спасибо за публикацию
Уважаемый Александр Валерьевич, Вы прочитали статью? Вот теперь Вы сможете написать научно мотивированное ходатайство суду и вынести мозг судье и эксперту.
Уважаемый Владимир Николаевич, да, прочитал! Поэтому и сказал — спасибо ;)
Уважаемый Владимир Николаевич, выносить мозг судье — занятие неблагодарное. Наша правовая система устроена так, что наиболее вероятно, скорее суд вынесет мозг адвокату своими дискреционными заявлениями: «у суда нет оснований не доверять», «суд не обладает специальными знаниями», «заключение эксперта не противоречиво и достоверно», «оснований для вызова и допроса эксперта нет».
наиболее вероятно, скорее суд вынесет мозг адвокатуУважаемый Николай Дмитриевич, ну вот, и Вам статья на пользу. Вы тоже, как эксперты, уже вероятность оценили. Правда, непонятно, как, но надеюсь научным методом
:)
Уважаемый Владимир Николаевич, эмпирическим методом. Он тоже строго научный!
Уважаемый Владимир Николаевич, спасибо за интересную публикацию! (Y)Вспоминаю дело пятнадцатилетней давности.Ох, как бы Вы мне тогда помогли. Мы тогда буквально на пальцах устанавливали обстоятельства столкновения двух машин.(headbang)
Уважаемый Владимир Николаевич,
должен ли судья привлечь эксперта для получения ответа на вопрос: в данном конкретном деле какие обстоятельства имели место — вероятные менее или вероятные более?
Уважаемый yewgeniy, вообще полагается, что заключение должно быть категоричным и цель судебной экспертизы не установить фактические обстоятельства, а отделить технически невозможные ситуации от возможных. Но от вероятности никуда не уйти, так устроен наш мир. Природа реализует наиболее вероятные сценарии. Пример — генетическая экспертиза.
Уважаемый Владимир Николаевич,
При этом суд принимает во внимание любые доказательства, с достоверностью подтверждающие происхождение ребенка от конкретного лица.не с вероятностью, а с достоверностью.
Но от вероятности никуда не уйти, так устроен наш мир. Природа реализует наиболее вероятные сценарии.Природа реализует разные сценарии: более вероятные и менее вероятные. Это прямо следует из того, что сценарии являются более вероятными или менее. Иначе природа не знала бы никаких более вероятных сценариев, а «реализовывала» бы единственный сценарий.
Если суд располагает только экспертным заключением о томи, что в рассматриваемой ситуации возможны разные обстоятельства (как такие, которые признаются более вероятными, так и такие, которые признаются менее вероятными), судья по-прежнему не знает, что случилось.
P.S. Во втором примере два разных объекта обозначены одним символом :)
Уважаемый yewgeniy, достоверность есть большая вероятность, см. любой учебник по теории вероятности.
Уважаемый Владимир Николаевич,
вопросы вероятности, раз уж они являются предметом изучения, требуют специальных знаний. Я ведь с чего начал? С вопроса: должен ли судья привлечь эксперта для получения ответа на вопрос: в данном конкретном деле какие обстоятельства имели место — вероятные менее или вероятные более?
Уважаемый yewgeniy, это вы, юрист, у меня, технаря, спрашиваете?! Незачет :)
Уважаемый Владимир Николаевич, огромная Вам от меня благодарность за подробное разъяснение значений приведенных понятий. Но в любом случае, суды к пояснениям юриста / адвоката в технических вопросах будут относиться скептически. Вроде: «Зачем Вы мне все это говорите, я этого не знаю и в этом не разбираюсь, вот нормы права я применить могу...». То есть даже на логику вроде: «у водителя иных причин замедлится до полной остановки, судя по дорожной ситуации, кроме как из-за удара сзади и не было вовсе» никак не реагируют.
У юриста иной процессуальный статус и даже если он понимает техническую сторону вопроса, выводы юриста именно по технической части какого-либо значения иметь не будут. Очень сомнительно, что приглашенный эксперт начнет рассчитывать степень вероятности своего вывода или хотя бы назовет обстоятельства на эту вероятность влияющие, а подвести его к ответу о некомпетентности в данном вопросе — это настолько высший пилотаж… до которого мне лично без помощи технического специалиста, мягко говоря, очень и очень далеко.
Поэтому степень вероятности до суда должен донести технический специалист. Особенно в ситуации, о которой указал уважаемый Александр Валерьевич — в отпуск уходят, то есть не хотят ответить «за свой базар». Так тем лучше. Если сам эксперт за свое заключение не отвечает, не отстаивает его, то другой, более компетентный в данном вопросе специалист суду может пояснить, что значит «наиболее вероятно». А может и выйдет, что данный вывод является ошибочным и «наиболее вероятна» другая ситуация.
Беда в том, что редко кто ТАКИХ специалистов привлекает к участию.
Уважаемый Сергей Равильевич, анализ Монте-Карло — существенно новый метод в нашей судебной и экспертной практике. Цель моей статьи — показать красоту математики, возможную область применения, призвать юристов обсудить где и как это можно применить в наших сегодняшних реалиях.
Вода точит камень. Более 18 лет назад я начал применять конечно-элементный анализ для расчетов затрат энергии на деформацию. У госов волосы дыбом вставали, пальцы топырились. А сейчас это установившаяся практика, хотя суды по-прежнему ничего не понимают в проекционно-сеточных методах.
Прочитал — толком ничего не понял. Но тут же на ум пришел анекдот: Маститому ученому и блондинке предложили ответить на вопрос: Каков процент вероятности того, что утром, выйдя на улицу, вы встретите динозавра?
Ученый погрузился в расчеты, таблицы и т.д. К вечеру вывел — 0,000001%
Блондинка, через секунду — 50%.
Как так, на чем вы основывали расчеты, сударыня!? Все просто — или встречу, или не встречу.
С 19 на 20 марта в машину жены (Ока) въехала «Приора». Гололед, Ока в мусорник, у Приоры капот погнут. Вот и смекаю, как бы «присобачить» сведения, изложенные в статье, к своему случаю, и ничего не получается:(
Уважаемый Владимир Николаевич, не согласитесь ли просто взглянуть на фотографию «Оки»? Может, что по направлению удара подскажете?
Я то пока свидетелей опрашиваю, да записи с камер ищу…
Уважаемый Владимир Александрович, конечно, я с удовольсвием взгляну на фотографию Оки, почешу затылок, и, как Ваша блондинка, сделаю вывод — либо Приора въехала, либо Ока :D
А в чем собственно, Ваш вопрос, только посмотреть?
Уважаемый Александр Валерьевич, Вы прочитали статью? Вот теперь Вы сможете написать научно мотивированное ходатайство суду и вынести мозг судье и эксперту. Уважаемый Владимир Николаевич, с такими познаниями этот мозг выносить станет проще! (Y)
Уважаемый Евгений Алексеевич, это точно. Пусть судья и не поймет про плотность вероятности и ее распределение. Но то, что эксперт нахимичил или не обосновал поймет. Ну а дальше главное при допросе — заставить эксперта мычать нечленораздельное при словах «распределение Гаусса» или «правило трех сигм».
:)
Чувствуется, что юристы недопонимают сути метода и перспективы его использования. Поясню «на пальцах».
Природа, среди множества физически возможных вариантов события, всегда реализует наиболее вероятный сценарий. Эксперт проводит расчеты по каким-то формулам, куда входят некие параметры. Эти параметры могут быть измерены или приняты экспертом с той или иной погрешностью, а фактически они принимают набор значений с равной вероятностью или значения с вероятностью согласно нормальному распределению.
Пусть у нас есть набор костей – монеты, на сторонах которых написано «да» или «нет», кубики с цифрами на гранях, аналогично октаэдры, шарики с плавно перетекающим цветом, обозначающим то или иное значение … Количество костей равно количеству параметров.
Берем все кости и кидаем. Записываем выпавший случайно набор параметров. И так – несколько десятков или сотен тысяч раз. Обнаруживаем, что определенный набор значений выпадает существенно чаще, в пределах дисперсии от максимума плотности вероятности – это и есть наиболее вероятный сценарий.
А если набор эксперта оказывается в зоне маловероятных значений, то следует соответствующий юридический вывод.
Уважаемый Владимир Николаевич, спасибо за красивую и познавательную статью!
На днях прошел допрос двух экспертов ФБУ СЗ РЦСЭ Минюста России, давших заключение по одному из простых видов ДТП, а именно столкновению 2-х авто, следовавших по правой полосе движения. При этом, исследовалась видеозапись видеорегистратора, установленного в кабине заднего автомобиля.
Госэксперты на задаваемые вопросы отвечали предложениями, которые сопровождались словами "скорее всего", "сейчас уже не помню", "думаю, что", "наверное", «это есть в литературе, но мы ее не привели, а точное название не помню», «эту программу мы использовали, потому что на семинаре кинематографистов она была рекомендована для применения», «производителя программы назвать не можем, мы ее скачали из Интернет, где она в свободном доступе».
И никакой вероятности! Похоже такого слова не знают (giggle)
Уважаемый Владимир Николаевич, после волшебного пенделя довольно сносно стал работать в MathCad, освоился в прикладной криминалистике транспортно-трасологической экспертизы расследования ДТП (сродни теории измерительных систем), вспоминаю курс теории погрешностей в информационно измерительной технике.
Изучил 154 приказ Минюста, чтобы говорить на понятном им языке.
При этом пришлось забросить все свои электронные проекты.
Скоро буду задавать умные вопросы.
после волшебного пенделя довольно сносно стал работать в ...Уважаемый Александр Валерианович, так я все время про то же говорю — пока утопаемый не начнет спасать сам себя, толку не будет. Иначе чхунов не перепрыгнуть
:)
Уважаемый Владимир Николаевич, огромное спасибо за статью. Разберусь обязательно, особенно с учетом Ваших пояснений. Сперва пугают математические выкладки да еще и с теорией вероятности (надеюсь я правильно понимаю), а потом ничего, даже интересно становится. Полагаю, что М.В. Ломоносов был прав про изучение математики и приведения в порядок ума. С уважением.
Уважаемый Андрей Владимирович, полностью с Вами согласен, разбираться с вероятностью надо, и использовать в свою пользу любое оружие.
В юриспруденции, когда подлежащий суду факт устанавливается на основании свидетельских показаний, он всегда остаётся, строго говоря, лишь вероятным, и необходимо знать, насколько эта вероятность значительна. В римском праве здесь принималось четверное деление: probatio plena (где вероятность практически переходит в достоверность), далее — probatio minus plena, затем — probatio semiplena major и, наконец, probatio semiplena minor. Необходимо отметить что в римском языке слово вероятность этимологически родственно слову честность.
Уважаемый Владимир Николаевич, спасибо за краткую но очень информативную лекцию, поместившуюся в несколько фраз комментария. С уважением.
Уважаемый Андрей Владимирович, нашел любопытную юридическую диссертацию о соотношении понятий «вероятность» и «достоверность».
В юриспруденции эти понятия могу, конечно, толковаться по своему. Но я писал о задачах физики. А в физике высокая вероятность есть достоверность. Пример — ваше тело состоит из колеблющихся в разных направлениях атомов. Есть вероятность того, что наступит момент, когда все атомы совершат колебание вверх, и… Но где это видано, чтобы адвокаты вот просто так летали?
Уважаемый Владимир Николаевич, по вашему какова вероятность заклинивания сателлита редуктора заднего моста на ТС BMW 530i, 2005 г.в. при касательном столкновении двух ТС, движущихся в попутном направлении. На BMW, кроме деталей оперения, повреждено ЛКП на ободе литого диска. Удар нанесен в момент, когда участок контакта располагался в верхней точке.
Уважаемый Николай Владимирович, так и посчитайте, что же Вы опять просите субъективную оценку. Мы же эксперты, а не метеорологи
Уважаемый Владимир Николаевич, меня и интересует Ваше субъективное мнение. Я смоделировал ситуацию, определил возможные перемещения рычагов подвески и полуоси, можно и глубже копать, определять возможные перемещения в разных плоскостях, мне не лень, но предела я не вижу. Или я не по теме?
какова вероятность заклиниванияУважаемый Николай Владимирович, а Вы как думаете, не будут ли все громко смяться, если я по Вашему описательному абзацу, почесав репу, выдам вероятность в процентах?
(giggle)
Уважаемый Владимир Николаевич, ответ да/нет меня вполне устроит. В любом случае, спасибо за ответы.
Остроумно и выглядит вполне научно :) Респект топикстартеру (hi)
Уважаемый Игорь Юрьевич, так разве теория вероятности у нас перестала быть наукой? Такого не слышал. Вот судебная экспертиза у нас, в России, официально давно перестала быть наукой. По этому поводу есть официальные документы.
А все эти наши приматы от юриспруденции виноваты. Даже поляки на 10 голов давно выше.
Владимир Николаевич, Вы почти правы, как всегда :), однако «наиболее вероятно» в выводах эксперта иногда имеет несколько иное значение. Например, я вижу на облицовке бампера отпечаток, который мне, на основании результатов измерения и опыта проведения аналогичных экспертиз, представляется отображением шарика фаркопа (устройства тягово-сцепного), однако я, напрягшись, смогу допустить, что это — отображение какой-то иной, неведомой (невиданной) мною редкой железяки или вообще копыта горного козла (giggle) Тут-то и напишется — от души и правда — «наиболее вероятно» :)
Уважаемый Игорь Юрьевич, можно написать просто «вероятно», в смысле «быть может». Хотя, если Вы оцените вероятность нахождения горного козла в Москве и вероятность наличия фаркопа у автомобиля, то Ваш вывод будет научным и строгим.
Уважаемый Владимир Николаевич, они столько не заплатят — считать вероятность козла :-) Кроме этого — нет таких специальных познаний — про козлов :) Это — совсем иные виды экспертиз :)
Да, беда Игорь Юрьевич. Получается, что если не заниматься козлами, то точно можно накозлить в экспертизе. Увы…
Могу поделиться маленькой уловкой.
Когда в заключении эксперта – автотехника я вижу волшебное слово «вероятно», в ходе допроса эксперта в суде я задаю вопрос о том, использовал ли он это «вероятно» в бытовом значении или в научном как эксперт. Ответить «в бытовом» — значит пилить сук, на котором он сидит, поставить под сомнение научность выводов. Узколобые эксперты постсоветского разлива, как правило, покупаются на это и отвечают: «в научном». Далее следует вопрос: Согласны ли Вы тем, что в научном понимании Вероятность – это отношение количества исходов, благоприятствующих данному событию, к общему числу равновозможных исходов. (Вероятностью случайного события A называется отношение числа n несовместимых равновероятных элементарных событий, составляющих событие A, к числу всех возможных элементарных событий N)?.. Эксперт вынужден согласиться. После этого следует добивающий вопрос о том, производил ли он вычисление вероятности.
Уважаемый Михаил Вениаминович, браво!!! Для этого я и писал статью!
(handshake)
Михаил Вениаминович, кроме Ваших, видимо, консультантов (или это — сами Вы — боюсь спросить?) или уважаемого топикстартера, конечно, редко кто «считает» вероятности. Тем не менее, наше Законодательство и существующие методики прямо указывают на то, что эксперт может пользоваться ещё и своим опытом (как судья — внутренним убеждением). Как-то выразить своё отношение к различным, иногда почти, простите, «равновероятным» версиям и помогает это — «наиболее вероятно». Ещё я юным экспертом слышал в судах от корифеев советской закваски монументальное и простое «этого не могло быть!» (giggle)
Уважаемый Игорь Юрьевич, я думаю, что в эпоху госдебилов ссылаться на советских корифеев как-то не прилично. Сегодняшние «корифеи» на глазок и с наибольшей вероятностью, как правило, решают задачки, которые корифеями тем и в снах не снились.
Уважаемый Игорь Юрьевич, вот-вот, часто эксперт сказанное им на допросе сопровождает словами «скорее всего», «сейчас уже не помню», «думаю, что», «наверное», «это есть в литературе, но мы ее не привели, а название книги не помню», «эту программу мы использовали, потому что она нам удобна и в Интернете она в свободном доступе".