Экспертиза ДТП. Точность прочностного исследования

После публикации статьи «Двойка за приговор, или как судья сам произвел экспертизу ДТП» появился комментарий праворубского новичка, всей душой разделяющего беспокойство экспертов МВД о численных методах. Простим ему, новичку, формулировку вопроса. Он, по смыслу, видимо, должен быть понят как «Какова точность Ваших расчётов (в процентном соотношении)?».

Такой вопрос, с видом отягощённого грузом истинных научных знаний авторитета, как правило, задают госэксперты дилетанты. Получается «Пастернака не читал, но скажу …». Однако, только на Праворубе уже опубликовано достаточно материалов, из которых можно сделать выводы о точности современных численных методов. Тем не менее, видимо, надо вернуться к вопросу о точности, чтобы поставить точку в этом вопросе и иметь материал для отсылки в будущем.

Кроме того, этот материал будет очень полезен адвокатам как для пополнения багажа своих знаний, так и для более полного понимания возможных экспертных задач по конкретному делу.

Ранее вопрос о точности прочностных расчётов так или иначе затрагивался в опубликованных на Праворубе статьях и судебной практике:

• «Консервная банка, или определяем затраты энергии на деформацию», где установлена высота падения молотка 265мм при фактической высоте 270мм (точность 98%);
• «Устанавливаем скорость наезда на пешехода по повреждениям автомобиля», где установленный расчётом интервал скорости наезда на пешехода совпал с результатами экспертизы по видеозаписи ДТП;
• «Экспертиза ДТП. Дело по ст. 264 УК РФ в Зазеркалье», где в итоге расчётное расстояние отброса грузовика влево в результате удара 29см хорошо совпало с расстоянием 28см до его следа на дороге от осевой линии (точность 97%);
• «Двойка за приговор, или как судья сам произвёл экспертизу ДТП», где расчётная скорость автомобиля 85 км/ч хорошо совпала со скоростью 86 км/ч, установленной другим экспертом с помощью другого метода (точность 99%).

Чтобы юридическая праворубская общественность не воспринимала упомянутые выше высокие показатели точности на веру в виде волшебной сказки, а понимала умом смысл дальнейших утверждений и примеров, далее будет правильным простым и понятным языком  1) постулировать целевую аксиому, 2) объяснить методологию, и 3) привести пример.

Сдаётся мне, что «Консервная банка» кое-кем никак не связывается с ДТП. Ну не могут они (эти кое-кто) мыслить абстрактно и провести параллель между повреждением банки от молотка и повреждением автомобиля от удара. К тому же вероятность с точностью путают, а возможно, и вообще законов физики не знают …

Аксиома

Целью судебной экспертизы ДТП является не установление каких-либо параметров движения автомобилей с некоторой точностью, а категоричное отделение технически возможных от технически невозможных ситуаций.   В голове человека, особенно после просмотра голливудских боевиков, может вообразиться всё, что угодно, что не может реализоваться в действительности, по меньшей мере, в том мире, в котором мы живем и совершаем ДТП, а не в некой параллельной реальности с иными мировыми константами. Это замечание весьма актуально для нашего судопроизводства (где каждый суслик – агроном), когда путём судоговорения нередко устанавливают такое, что не и снилось тем же голливудским режиссёрам.

Например, известный вопрос к водителю дорожного катка: «Ну, расскажи, как ты Мерс обгонял, как подрезал?»

Из приведённой аксиомы следует задача эксперта – принимая возможные крайние значения  исходных и нормативных данных (массы, коэффициенты сцепления шин с дорогой, механических свойств материалов и т.п.) установить техническую границу возможного, внутри которой уже будут разбираться юристы.

Поэтому говорить о точности результатов экспертизы ДТП здесь не имеет смысла, так как границы возможного эксперт обязан очертить категорично. Можно говорить о том, сколь велика область возможного, установленная экспертом, и как её можно сузить. Для одной экспертной задачи может быть и нужны металловедческие исследования, чтобы установить механические свойства секретной немецкой стали, а для другой – не нужны, так как достаточно принять минимальные свойства обычной конструкционной стали. При этом влияние погрешности в сочетании с другими факторами либо будет мало, в пределах разумной погрешности, либо не повлияет на выводы эксперта даже при установленном широком диапазоне возможного интервала параметров движения транспортных средств. 

Вывод. Нужно ли для конкретной экспертной задачи «вешать колбасу в граммах или в миллиграммах», определяет и обосновывает сам эксперт исходя из того, сможет ли он при этом категорично ответить на поставленные ему вопросы.
Замечание. Утверждать, что заключение эксперта по ДТП неверно, так как эксперт не определил (или невозможно определить) свойства зарубежного материала или с микронной точностью не установил форму детали всё равно, что утверждать о невозможности расчета скорости по длине тормозного следа из-за того, что эксперт не учёл рисунок и глубину протектора на шине. Но на самом деле эксперт учёл только коэффициент трения материала о материал (резины о дорогу) и, тем самым, установил наименьшую скорость. Всё, что по мнению «знатоков», надо учесть, в данном случае пойдёт только в плюс установленной скорости. 

Методология численных расчетов

Заслуга Ньютона перед человечеством не только в его законах физики. Ньютон открыл бесконечно малые – он разработал дифференциальное и интегральное исчисление, или аппарат исследования, без которого не было бы научно-технического прогресса. Суть и применение этой методологии к экспертизе ДТП сейчас будет просто и популярно изложена для юристов. Начнём с отвлечённой задачи, только для усвоения смысла.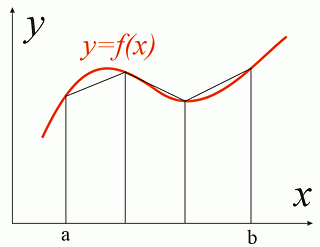

Изобразим в декартовой системе координат некую кривую – график некоторой функции f(x). Задача – вычислить площадь под кривой в интервале [ab] с заданной точностью (погрешностью).

Сначала разобьём, например,  интервал [ab] на три участка, как на рисунке. Получаем три трапеции, площади которых мы считать умеем, что и сделаем, а потом их сложим. Получили первое приближение площади под кривой.

Теперь разобьём интервал [ab] на четыре участка и проделаем то же самое. Потом – на пять, шесть, …, сто, …. Вычисляя каждый раз сумму площадей трапеций заметим, что при достаточно большом количестве разбиений эти суммы почти не отличаются друг от друга. Разница между ними и есть погрешность определения искомой площади под кривой. Поэтому надо остановиться, когда точность (или погрешность) станет меньше или равна заданной. 

То, что мы сейчас усвоили, называется методом трапеций для численного вычисления определенного интеграла.  Это мы все проходили когда-то в школе.

Примерно так же производится и численный расчет деформаций некоторого объекта. Возьмёмся посчитать результат удара некоторой коробки, которая на рисунке.

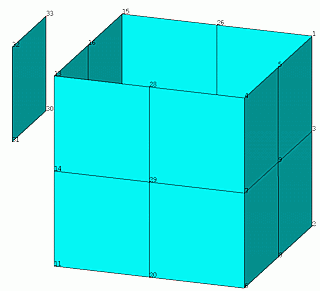У нашей коробки 5 квадратных граней – 4 стороны и дно, а верх открыт. Слева – жёсткая неподвижная стенка, в которую потом ударится наша коробка. Мысленно разобьём каждую грань на четыре части, и назовём каждую часть элементом, а углы элемента – узлами.

Рассмотрим один простейший элемент с узлами A, B, C и D. Положим, что линии AB, BC, CD и DA – это прямые и всегда останутся прямыми. Если расстояние между линиями, например, AB и CD увеличится, то получаем растяжение нашего элемента, а уменьшится – сжатие. Так же легко представить себе кручение в виде закручивания линии, например, AB относительно CD, или сдвиг как перемещение линии AB вдоль неё самой относительно линии CD. Всё, что мы можем проделать с простейшим элементом, называется испытаниями, а все испытания материалов давно ГОСТированы. Поэтому силы, возникающие в узлах A, B, C и D при том или ином испытании или их сочетаниях, для каждого материала легко определяются, и соответственно, легко определяется величина затраченной энергии.

Заметим ещё, что, например, узел A для нашего элемента – это, в общем случае, и узел его соседа. Поэтому перемещение любого узла вызывает реакцию в соседних элементах, а силы реакции в узлах соседей вызывают реакцию дальше у их соседей и т.д. Примерно так же, как трогается железнодорожный состав. Локомотив трогается, зазор в сцепном узле выбирается, и локомотив увлекает за собой первый вагон, потом локомотив и первый вагон уже вместе трогают с места второй вагон, потом локомотив и два первых вагона вместе трогают третий вагон и т.д.  То есть специалист может связать перемещения каждого узла с перемещениями его соседей некоторыми уравнениями.
Так как узлов много, то много и уравнений связи. Какие это уравнения и как они составляются – это сугубо техническая задача, юристам над этим голову ломать не надо.

Зададим всем узлам нашей коробки некую одинаковую начальную скорость в сторону стенки, или кинетическую энергию. Зададим граничные условия в виде условия: узлы не могут пройти сквозь стенку, но могут скользить вдоль неё (коэффициент трения задаём тоже) или отходить назад. На самом деле граничные условия – это корректировка уравнений связи узлов между собой.

А теперь смысл задачи. Итак, все узлы связаны со своими соседями соответствующими уравнениями, а граничные условия заданы. Тогда компьютер, под управлением умной программы, выполняя принцип Лагранжа найдет для каждого момента времени такое взаимное положение узлов, при котором обеспечивается минимум затрат полной энергии – суммы работ внешних и внутренних сил. И это взаимное положение узлов будет истинным в данном приближении, так как таков наш мир – самопроизвольно реализуются процессы с наименьшими затратами энергии. 

Смотрим результат для нашей коробки с некоторым шагом во времени.

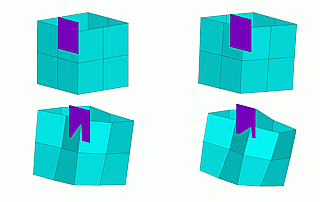Грубо, конечно, как и вычисление площади под кривой тремя трапециями, но похоже на правду. Что дальше? А то же, что и с трапециями. Увеличиваем количество элементов, а потом ещё раз увеличиваем.

Замечаем, что разница расчётных затрат энергии между двумя последними расчётами не превышает 2%. Такой точности вполне достаточно, дальше измельчать сетку элементов нет необходимости, и расчёт закончен. Заметьте, что последняя картинка здорово похожа на правду, даже зазубрины от края стенки отобразились на ребре!

Теперь юристу должен быть понятен смысл конечно-элементного расчёта – объект в конкретных условиях деформируется не как попало, а так, что среди возможных его деформаций (изменений формы), какие только можно и нельзя себе вообразить, находится такая, которая обеспечивает минимум полной энергии системы объект-препятствие.

Вывод. Численные методы идеальны для решения судебно-экспертных задач, так как имеют такое свойство как сходимость. Это означает, что любой расчёт можно произвести либо с заранее заданной точностью, либо проконтролировать фактическую точность данного расчёта.

Замечание 1. Исходя из постулированной выше аксиомы, результат расчёта для данной, например, коробки, категоричен и даёт наибольшую возможную скорость удара, если эксперт использовал наибольшие возможные механические характеристики материала, или наоборот — наименьшую  возможную скорость удара, если эксперт использовал наименьшие возможные механические характеристики материала.

Замечание 2. Никто не мешает использовать для расчёта сложный объект или объекты, состоящие из множества деталей из разных материалов каждый. Да и вообще, каждый элемент может быть представлен разными механическими характеристиками. Вот вам и коррозия, и заплатки, и всё, что только не придумаете. Но лучше всего посмотреть работы сотрудников NCAC – Национального центра анализа ДТП при университете имени Джорджа Вашингтона. По этой ссылке читатели могут просмотреть ряд анимаций. Это – не работа художников, это – анимация расчётных результатов. На этом сайте и некоторых других есть статьи и видеоклипы, когда те же машины в натуре сталкиваются между собой и с препятствиями. Сходство результатов расчёта и натурных испытаний потрясающее! Можно посмотреть и этот ролик на YouTube. Это тоже расчёт методом конечных элементов. Таким образом, мировая наука не стоит на месте, не ждёт «утверждения в установленном порядке» от МВД РФ или МЮ РФ, а просто про них и про их мнение даже и не думает. Однако, полный обзор работ иностранных учёных – большая тема отдельной статьи.

Дополнение (можно пропустить). Конверсия оборонных технологий приводит, подчас, к совершенно неожиданному применению.  И консервная банка или ДТП здесь – не единственные примеры. Когда моя дочь училась в старших классах, стало модным проводить научно-исследовательские конференции школьников. Но ведь исследование – это получение новых знаний, а не списывание. Дочь попросила совета по теме исследования, а в это время сын гонял по коридору новый футбольный мяч. Я и посоветовал исследовать мяч – почему мяч, сброшенный с высоты 1 м даже на твёрдый и гладкий бетонный пол, поднимается вверх только на 90 см с небольшим. Куда девается энергия? Сопротивление воздуха, разогрев и внутреннее трение камеры мяча об оболочку, как обычно объясняют «знатоки», – это слишком мало для исчезнувшей куда-то энергии мяча.

Конечно, я помог сделать конечно-элементную модель  мяча. То, что выяснилось исследованием, стало, во-первых, предметом обсуждения солидных учёных в Институте механики РАН, а во-вторых, объектом патентования. Пожалуйста – Патент РФ (если патент не загрузится сразу, нажмите кнопку «обновить» в вашем браузере или Ctrl+F5) на изобретение №2306162 «Игровой мяч». А численным исследованием выяснилось то, что мяч при ударе об пол в самом нижнем своём положении теряет контакт своего нижнего полюса с полом, т.е. его «попка» прогибается вовнутрь (вверх), и мяч контактирует  с полом только по периметру окружности. И в этом-то положении он и отрывается от пола, а восстановление шарообразной формы мяча происходит уже в воздухе. Поэтому эта часть энергии  как бы теряется, потому что она не используется для взлёта. Этот недостаток и был исправлен в вышеуказанном патенте.

Так что, вокруг нас есть много вещей, до которых ещё не дошли руки и головы исследователей. А современные численные модели совершенны в такой степени, что пригодны для широчайшего круга исследований самой модели, а не натурного образца. Результаты исследования уже потом проверяются экспериментом. 

Простой и понятный пример

Пикап ехал по главной дороге в затяжном повороте. Справа на дорогу выехал ВАЗ-2106 и своим передним правым углом ударил в заднюю правую часть пикапа. В результате удара пикап развернуло по часовой стрелке, и он выехал в кювет, где опрокинулся.

Это пикап: 

А это его обидчик, ВАЗ-2106:

Если читатель не обратил внимания на трубу под задней частью пикапа, то страховщики были более внимательны. Появился вопрос, почему эта труба не повреждена, и следов от неё нет на машине виновника?

Это совмещение аналогичного по габаритам автомобиля с пикапом. Видно, что вопрос страховщиков вполне обоснован.

Вывод трасолога полностью основан на судебно-экспертной методике, применяемой МЮ РФ и МВД РФ – пикап стоял, а «шестёрка» его легонько стукнула, чтобы создать следы ДТП. То есть – налицо имитация ДТП с целью получения страховки. Фрагмент методики РФЦСЭ ниже.

Возможно, для многих адвокатов этот абзац из методики транспортно-трасологической экспертизы станет откровением. Оказывается, трасологи МВД и МЮ работают на основе гипотезы, и их выводы могут быть только вероятны по определению! Их и надо спрашивать про вероятность их результатов!

Головы многих, даже очень хороших экспертов, засорены ложными представлениями. Это свойство человеческого мышления, и ничего страшного здесь нет. Когда-то все думали, что Земля плоская и стоит на трёх китах. Так же после просмотра роликов NCAC может засориться и голова читателя. Засориться тем, что читатель будет полагать, что для анализа столкновения пикапа и «шестёрки» нужны их полные конечно-элементные модели, от переда до багажника. Но это не так. В контакт вступали всего одна панель пикапа и угол «шестёрки». Для определения величины силы удара нужна только одна из этих деталей. А для дальнейшего расчёта движения автомобилей под действием силы удара достаточно знать только габариты автомобилей, их массы, и коэффициент сцепления шин с дорогой.

По заявлению страховой компании я проверил это ДТП. Результат прочностного расчёта части стенки кузова пикапа показал, что для получения такой деформации глубиной до 7 см требуется сила не менее 4 тонн. Почему «не менее»? А потому, что исследовать японскую сталь не было необходимости, в расчёте приняты наименьшие механические свойства конструкционной стали. На рисунке ниже показано расчётное поле поперечных перемещений. 

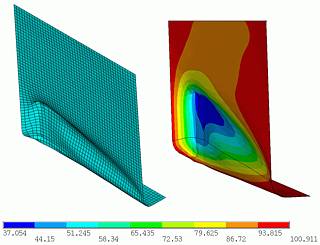Теперь,  призвав на помощь Ньютона и его дифференциальные уравнения движения, решаем задачу движения машин при ударе с силой взаимодействия 4 тонны, и глубине деформации 7 см.

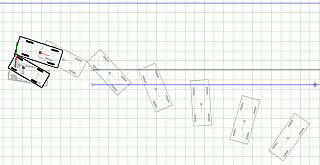На рисунке выше показано расчётное движение пикапа и «шестёрки». Посмотрим на правый задний угол пикапа и передний правый угол «шестёрки» в более крупном масштабе. На рисунке ниже (размер координатной сетки 10см) показан момент наибольшего взаимного внедрения машин на глубину в пикап 7 см. Сверху контур задней части пикапа, снизу контур передней части «шестёрки». Зелёная линия – сила, скользящая вдоль кузова пикапа и действующая на пикап, красная линия – такая же сила, но действующая на «шестёрку». 

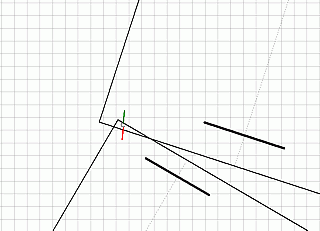А это то, что случилось через мгновение – машины разошлись под действием силы удара.

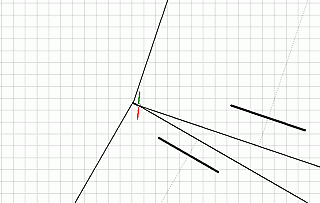Вывод.  Прочностного расчёта неполной части одной детали кузова пикапа с наименьшими возможными механическими характеристиками материала оказалось достаточным, чтобы сделать категоричный вывод о том, что пикап и «шестёрка» были отброшены друг от друга в результате удара, а труба в нижней части пикапа и край крыла «шестёрки» разминулись в пространстве. Если механические свойства стали пикапа были выше, то сила взаимодействия была больше, а отброс машин друг от друга произошёл раньше.

Интересна ли теперь кому-нибудь точность (погрешность) расчёта или фактическая величина силы взаимодействия этих машин?  Думаю, что нет. 

Итог

Подводя итог публикации, отвечаю на вопрос «Какова точность Ваших расчётов (в процентном соотношении)?» 

Точность будет такая, какую закажете. Вопрос лишь в трудоёмкости работы и цене, а технических пределов нет. Закажете расчёт с погрешностью 0.0000000001% – сделаем!

Первый год  — осмотр, разборка, измерения, металловедческие и материаловедческие экспертизы всех деталей машины, второй и третий года – расчёты, четвёртый год – составление заключения.

Автор надеется, что после прочтения этой статьи, в совокупности с предыдущими публикациями, у юристов сложилось более-менее целостное представление о современных технических методах реконструкции обстоятельств ДТП. 

PS.Осталось дать ответ и на предположение новичка-комментатора «Может быть МВД не принимает данной методики расчетов скорости, поскольку …» тоже отвечаю, и, надеюсь, что юридически грамотно.

А разве, уважаемый новичок, кто-то предлагает блюдечко с голубой каёмочкой МВД РФ или МЮ РФ? Ни я, ни РАН ничего им не должны, и мы не печёмся денно и нощно об их благополучии. Поскольку способ защищен Патентом РФ (если патент не грузится сразу, нажмите кнопку «обновить» в вашем браузере или Ctrl+F5) на изобретение №2308078, ни МВД РФ, ни МЮ РФ или кто-либо другой не смогут законно использовать указанный способ расчёта столкновений транспортных средств на территории РФ, пока не купят лицензию в установленном законом порядке у правообладателя. Вы что-то напутали, уважаемый новичок. Времена СССР (раньше думай о Родине) прошли, и всё переведено на принцип «утром деньги, вечером стулья». Автора его «стулья» пока вполне устраивают, а будет мало, изобретём ещё.