Как бы то ни было, метод Эйлера, простейший численный метод решения дифференциальных уравнений, как таковой до сих пор не нашел своего применения в Минюсте, их ученым советом не апробирован и не утвержден. Хотя те, кто так говорит, сами ничего не знают.
Метод Эйлера, как и ему подобные методы, применяются в экспертизе ДТП. Поэтому эта статья полезна для автоэкспертов и адвокатов тем, что в ней просто и ясно показано, как работает модель движения автомобиля в специальных компьютерных программах реконструкции ДТП, типа PC-Crash. А это позволяет, при необходимости, сформулировать ряд вопросов для экспертного исследования или задать несколько неприятных вопросов эксперту.
Решаем простейшее дифференциальное уравнение
Адвокаты (про госавтоэкспертов точно не скажу), возможно, помнят из школьной программы, что такое производная функции. Производная – это тангенс угла наклона касательной к графику функции в некоторой точке. Это ее геометрический смысл.
Если наша функция есть зависимость пути от времени, то производная – это зависимость скорости от времени. Вторая производная от пути по времени – это зависимость ускорения от времени.
Большей информации для задачи движения автомобиля нам не надо.
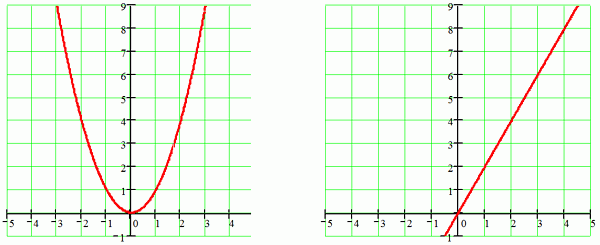
Для иллюстрации метода Эйлера рассмотрим некоторую функцию y(x)=x2. Ее график показан выше слева, это – парабола. Справа на рисунке – график производной этой функции y’(x)=2x.
Видно, что, например, при x=0 производная y’=0, или касательная параллельна оси абсцисс. А при x=2 производная y’=4, или в этой точке тангенс угла наклона функции y(x) равен 4, откуда угол наклона касательной составляет около 76 градусов. Если сама функция y(x) нам не известна, а известна только ее производная, то получить эту функцию можно интегрированием производной.
Если мы проинтегрируем производную аналитически, то получим формулу искомой функции y(x), а если численно – только ее график в виде набора точек. Давайте проинтегрируем численно методом Эйлера.
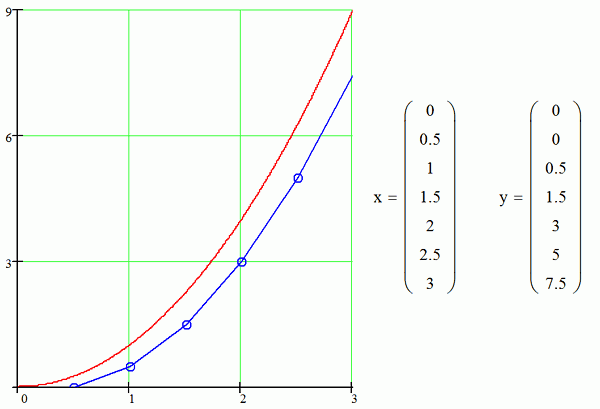
Полагаем, а это – граничные условия, что искомая функция начинается с точки x=0 и y=0. Наша задача – получить правую ветвь этой параболы.
Принимаем шаг интегрирования dx=0.5. Тогда в этой точке, при x=0, значение производной тоже равно нулю 2x=2x0=0, и мы попадаем в следующую точку x=0+0.5=0.5 и y=0+2x0x0.5=0. В этой второй точке x=0.5 значение производной уже равно 2х0.5=1, поэтому далее мы попадаем в третью точку с координатами x=0.5+0.5=1 и y=0+1x1x0.5=0.5. И так далее.
Табличка со значениями аргумента x и функции y, а так же график реальной функции y=x2 (красный цвет) и ломанной (синий цвет), полученной методом Эйлера показан на рисунке ниже.
 Как видно из сравнения двух графиков, погрешность велика. Но и шаг интегрирования dx=0.5 был выбран большой. Если уменьшить шаг интегрирования, уменьшится и погрешность.
Как видно из сравнения двух графиков, погрешность велика. Но и шаг интегрирования dx=0.5 был выбран большой. Если уменьшить шаг интегрирования, уменьшится и погрешность.Это называется сходимостью метода – при уменьшении шага возрастает точность. Сравнивая два решения с разным шагом, можно сделать вывод о погрешности полученного решения. А сейчас, с современными компьютерами, проблем с выбором весьма малого шага интегрирования нет, так как человеку все равно, длился расчет 0.1 секунды или 0.01 секунды, лишь бы не часами.
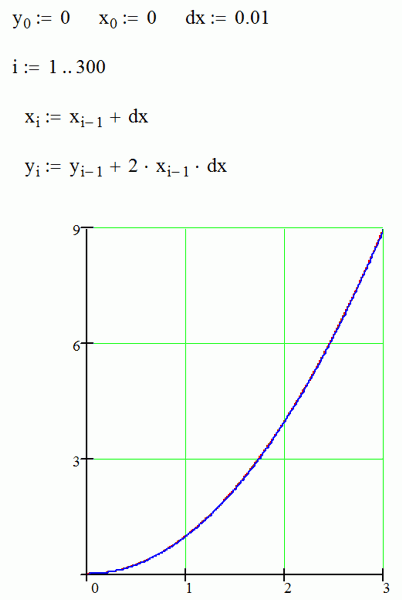
Для примера на следующем рисунке показан результат интегрирования с шагом dx=0.01, и видно, что красная и синяя линии практически слились. Там же показана программа расчета: задаем начальную точку и шаг интегрирования, а далее в цикле для параметра i, пробегающего значения от 1 до 300 идет расчет точек ломаной по методу Эйлера.
Интегрируем дифференциальные уравнения движения автомобиля
Рассмотрим решение задачи движения полностью заторможенного автомобиля Ауди массой m=1185 кг, моментом инерции I=1566.4 кг ·м2, по горизонтальной поверхности с коэффициентом сцепления колес с поверхностью дороги f=0.7 (сухой асфальт). Скорость автомобиля в начальный момент v0=30 км/ч в направлении вправо на рисунке, скорость вращения w0=3c-1 (радиан в секунду). Такое движение может быть как в результате удара и тогда это движение после разделения автомобилей, либо занос в колее и т.п.
На рисунке ниже показано решение этой задачи в программе PC-Crash (рекомендованной Минюстом).
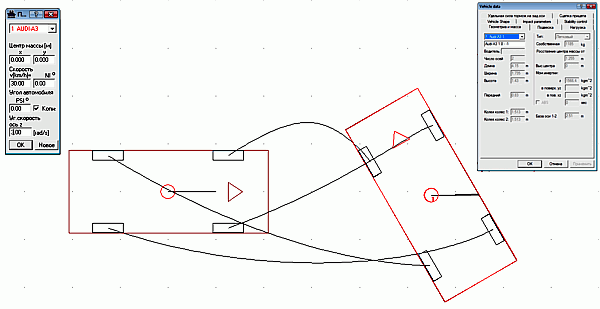 Табличка справа содержит параметры автомобиля, а слева – указанные начальные скорости. Точки на рисунке – координатная сетка с шагом 1м. В начальный момент времени центр тяжести автомобиля находится в точке с координатами x=0, y=0. Угол между продольной осью автомобиля и осью координат x (направлена вправо на рисунке) a=0.
Табличка справа содержит параметры автомобиля, а слева – указанные начальные скорости. Точки на рисунке – координатная сетка с шагом 1м. В начальный момент времени центр тяжести автомобиля находится в точке с координатами x=0, y=0. Угол между продольной осью автомобиля и осью координат x (направлена вправо на рисунке) a=0.Начальное значение времени положим t=0, шаг интегрирования по времени dt=0.001 сек. Мы не знаем значения ускорений центра тяжести автомобиля вдоль координатных осей и угловое ускорение в начальный момент времени, поэтому их значения полаем также равными нулю: acx=0, acy=0 и e=0.
Далее будем считать, что левой переднее колесо автомобиля – это колесо 1, правое переднее – 2, правое заднее – 3 и левое заднее – 4. С помощью таблички с параметрами автомобиля определим начальные координаты его колес: x1=1.25 м, y1=0.755 м, x2=1.25 м, y2=-0.755 м, x3=-1.26 м, y3=-0.755 м, x4=1.26 м, y4=0.755 м. Для расчетов нам понадобятся длины и углы с осью x радиус-векторов всех колес.
Для передних колес это R1=1.46 м, для задних – R2=1.469 м, и углы а1=0.543 рад (31.13 град), а2=-0.543 рад (-31.13 град), а3=3.68 рад (210.9 град), а4=2.6 рад (149 град). Все исходные данные приведены в листинге ниже.
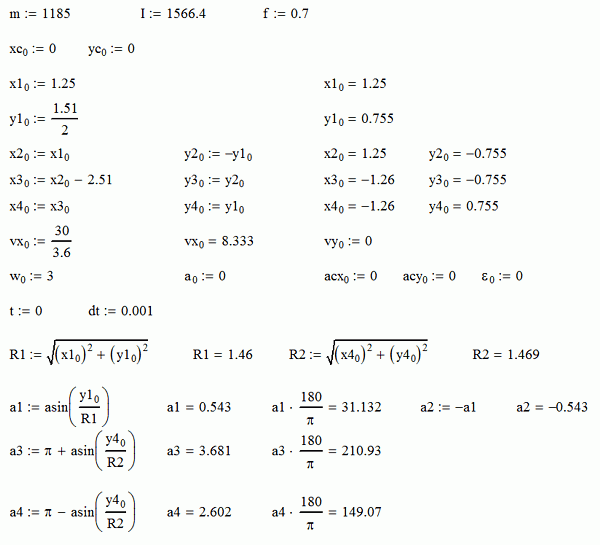 Движение автомобиля в плоскости определяется вторым законом Ньютона в форме дифференциальных уравнений второго порядка (то есть содержащих вторые производные, или производные от производных), из которых два первых – для центра тяжести автомобиля (x и y – координаты центра тяжести), а третье – для вращения автомобиля вокруг его центра тяжести (а – угол между продольной осью автомобиля и координатной осью x). В запись этого закона Ньютона также входят сумма проекций сил сцепления всех колес на оси координат x и y, суммарный момент сил сцепления всех колес относительно центра тяжести, масса автомобиля и его момент инерции относительно вертикальной оси, проходящей через центр тяжести.
Движение автомобиля в плоскости определяется вторым законом Ньютона в форме дифференциальных уравнений второго порядка (то есть содержащих вторые производные, или производные от производных), из которых два первых – для центра тяжести автомобиля (x и y – координаты центра тяжести), а третье – для вращения автомобиля вокруг его центра тяжести (а – угол между продольной осью автомобиля и координатной осью x). В запись этого закона Ньютона также входят сумма проекций сил сцепления всех колес на оси координат x и y, суммарный момент сил сцепления всех колес относительно центра тяжести, масса автомобиля и его момент инерции относительно вертикальной оси, проходящей через центр тяжести.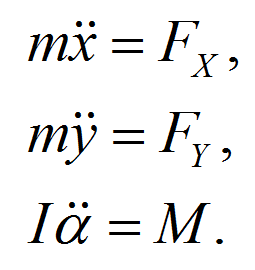 Ну а далее тот самый цикл, на каждом шаге которого время прирастает на 0.001 секунды в интервале от 0 до 1.35 секунды, а координаты центра тяжести автомобиля и его курсовой угол постоянно пересчитываются исходя из приведенных выше дифференциальных уравнений движения в плоскости.
Ну а далее тот самый цикл, на каждом шаге которого время прирастает на 0.001 секунды в интервале от 0 до 1.35 секунды, а координаты центра тяжести автомобиля и его курсовой угол постоянно пересчитываются исходя из приведенных выше дифференциальных уравнений движения в плоскости.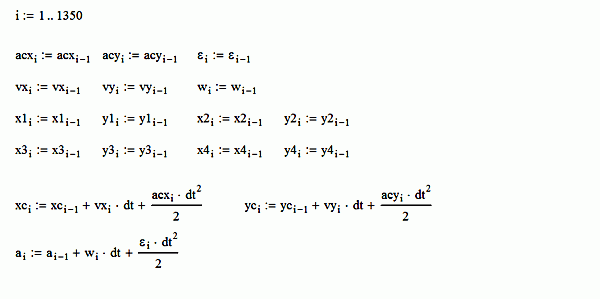 Внутри цикла, на i-м шаге, значения ускорений и скоростей автомобиля и координаты его колес принимаются из прошлого i-1 –го шага, и делается первый (черновой) расчет положения центра тяжести и курсового угла на текущем шаге (две последние строки на рисунке выше – формулы известны из школьного курса физики и являются результатом аналитического интегрирования дважды дифференциальных уравнений движения). Это необходимо для определения направления движения колес автомобиля, чтобы знать, в каком направлении приложить этим колесам векторы сил сцепления автомобиля с дорогой. Получается, что в таком алгоритме направление сил сцепления берется с запаздыванием по времени на величину шага интегрирования. Но это не страшно, так как шаг по времени очень мал.
Внутри цикла, на i-м шаге, значения ускорений и скоростей автомобиля и координаты его колес принимаются из прошлого i-1 –го шага, и делается первый (черновой) расчет положения центра тяжести и курсового угла на текущем шаге (две последние строки на рисунке выше – формулы известны из школьного курса физики и являются результатом аналитического интегрирования дважды дифференциальных уравнений движения). Это необходимо для определения направления движения колес автомобиля, чтобы знать, в каком направлении приложить этим колесам векторы сил сцепления автомобиля с дорогой. Получается, что в таком алгоритме направление сил сцепления берется с запаздыванием по времени на величину шага интегрирования. Но это не страшно, так как шаг по времени очень мал.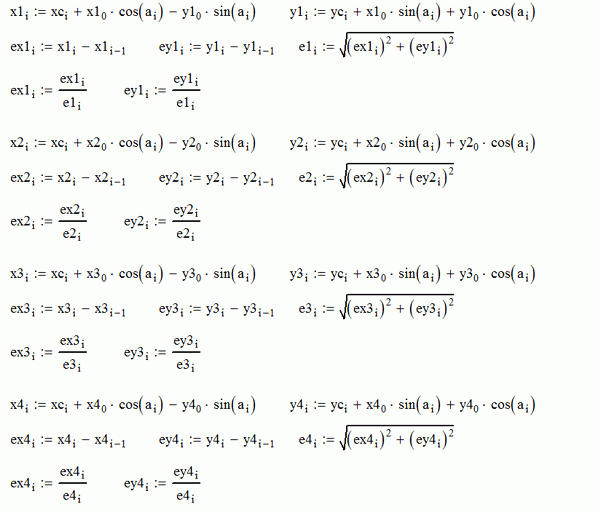 Далее, как показано на листинге выше, исходя из текущего положения центра тяжести автомобиля и его курсового угла, путем сравнения глобальной системы координат и системы координат автомобиля (документ, как это делать, приложен к статье), определяются текущие координаты каждого колеса автомобиля. Сразу же вычисляются единичные векторы (орты, как это называется в аналитической геометрии) направления движения каждого колеса автомобиля, чтобы затем приложить силы сцепления в противоположном им направлениям.
Далее, как показано на листинге выше, исходя из текущего положения центра тяжести автомобиля и его курсового угла, путем сравнения глобальной системы координат и системы координат автомобиля (документ, как это делать, приложен к статье), определяются текущие координаты каждого колеса автомобиля. Сразу же вычисляются единичные векторы (орты, как это называется в аналитической геометрии) направления движения каждого колеса автомобиля, чтобы затем приложить силы сцепления в противоположном им направлениям. Остается, как видно из листинга выше, вычислить величину силы сцепления с дорогой на каждом колесе исходя из ¼ массы автомобиля и коэффициента сцепления шин с дорогой.
Остается, как видно из листинга выше, вычислить величину силы сцепления с дорогой на каждом колесе исходя из ¼ массы автомобиля и коэффициента сцепления шин с дорогой.При реальном расчете эксперт может принять и иные соотношения. Так же вычисляются проекции сил сцепления на каждом колесе на оси глобальной системы координат как произведение величины указанной силы на компоненты ортов направления движения колеса со знаком «минус».
После этого (в пятой строке) проекции всех сил на оси координат суммируются. Далее вычисляется момент этих сил относительно центра тяжести как векторное произведение сил сцепления на радиус-вектор каждого колеса.
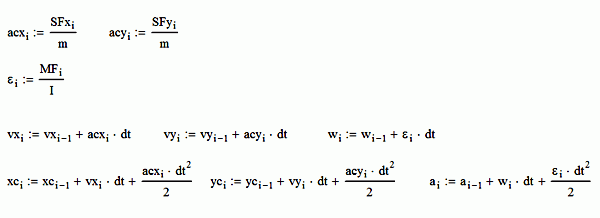 Теперь остается вычислить из второго закона Ньютона реальное ускорение (если получится отрицательным, то это – замедление) центра тяжести автомобиля и его угловое ускорение на текущем шаге, из них реальные скорости центра тяжести в проекции на оси координат и скорость вращения автомобиля, и реальные координаты центра тяжести и курсового угла автомобиля на текущем шаге. Реальные потому, что выше, для определения направления сил сцепления на каждом колесе эти значения принимались их предыдущего шага интегрирования. Листинг показан выше.
Теперь остается вычислить из второго закона Ньютона реальное ускорение (если получится отрицательным, то это – замедление) центра тяжести автомобиля и его угловое ускорение на текущем шаге, из них реальные скорости центра тяжести в проекции на оси координат и скорость вращения автомобиля, и реальные координаты центра тяжести и курсового угла автомобиля на текущем шаге. Реальные потому, что выше, для определения направления сил сцепления на каждом колесе эти значения принимались их предыдущего шага интегрирования. Листинг показан выше.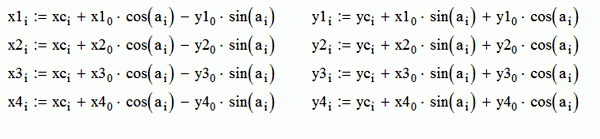 Последнее, что осталось, это вычислить реальные положения колес на текущем шаге интегрирования, как показано на листинге выше.
Последнее, что осталось, это вычислить реальные положения колес на текущем шаге интегрирования, как показано на листинге выше.Интегрирование закончено.
Проверяем результаты
Результат интегрирования в данном случае это таблица, содержащая 1351 строку, в столбцах которой содержатся все те величины, которые мы рассчитали, то есть имеющие в листингах нижний индекс i. Таблица сама по себе суду ничего не дает, хотя некоторые адвокаты, услышав про нее, требуют представить, что я с удовольствием делаю – представляю на электронном носителе. Но лучше визуализировать результат в виде расчетного положения автомобиля в разные моменты времени и траектории его колес. В программе выше мы не вычисляли положения углов автомобиля, поэтому представим в виде графика расчетные траектории всех 4-х колес автомобиля с координатной сеткой 1м.
На рисунке ниже траектория левого переднего колеса красная, правого переднего синяя, правого заднего фиолетовая, левого заднего черная.
 И, наконец, самый главный вопрос – а что мы тут насчитали? Для ответа на него ниже масштабно совмещены рисунок из программы PC-Crash и результат нашего домашнего расчета. Сравнение показывает, что с помощью программы выше получен тот же самый результат, так как траектории колес полностью совпали.
И, наконец, самый главный вопрос – а что мы тут насчитали? Для ответа на него ниже масштабно совмещены рисунок из программы PC-Crash и результат нашего домашнего расчета. Сравнение показывает, что с помощью программы выше получен тот же самый результат, так как траектории колес полностью совпали.
Обсуждение результатов
Итак, приведенный пример расчета движения заторможенного автомобиля в заносе показал, что не боги горшки обжигают, и развеял мрак тайны специальных компьютерных программ. Это немаловажно как для экспертов, так и для адвокатов, так как, надеюсь, с учетом цикла статей по алгоритму CRASH3 и уравнениям движения им стало понятно, как это все работает. Понятно тем, кто это читает. А остальным?
Для чего может понадобиться такой «ручной» расчет? Он нужен, когда положения колес автомобиля после удара существенно отличаются от их положений до удара, когда одно колесо оторвано, когда колеса после удара смотрят в разные стороны, когда одно колесо или больше спущено, когда некоторые из колес заклинены деформированными частями автомобиля, а другие свободно или со скрежетом вращаются. И это только небольшое число случаев из тех, которые могут возникнуть в реальном ДТП, и не могут быть учтены той или иной компьютерной программой.
Выше рассмотрено движение полностью заторможенного автомобиля, поэтому модель шин была простейшей – силы сцепления колес были направлены против направления движения каждого колеса. А если в реальности по другому? Какая и почему использована модель в конкретном расчете?
Резюмируя, можно сказать снова и снова – лишними знания не бывают, и теорию знать полезно.




Уважаемый Владимир Николаевич, к сожалению лично мне не приходилось встречать специалистов, способных на подобные расчеты или даже представляющих себе в чем их суть.
Современные «эксперты» способны максимум на вывод вроде: «если автомашина Ниссан Кашкай двигалась 2 секунды после начала торможения первичным было столкновение между Хюндай и Лада Калина, если 3 секунды, первичным было столкновение между Лада Калина и Ниссан Кашкай» (это уже с учетом показаний водителя Ниссана о том, что он тормозил после удара 2-3 секунды).
или даже представляющих себе в чем их сутьУважаемый Сергей Равильевич, вот она — суть судебной экспертизы в нашей стране!
:)