Адвокатам же будет интересно узнать, что при наличии современного компьютера одних только уравнений движения достаточно для анализа движения автомобиля, а в остальных формулах просто нет необходимости. Это дает возможность легко проверить решение автоэксперта, полученного с использованием программы типа PC-Crash или иным способом.
Интересно, как сам Ньютон сформулировал свой 2-й закон:
Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.
Если какая-нибудь сила производит некоторое количество движения, то двойная сила произведет двойное, тройная – тройное, будут ли они приложены разом все вместе, или же последовательно и постепенно. Это количество движения, которое всегда происходит по тому же направлению, как и производящая его сила, если тело уже находилось в движении, при совпадении направлений прилагается к количеству движения тела, бывшему ранее, при противоположности – вычитается, при наклонности – прилагается наклонно и соединяется с бывшим ранее, сообразно величине и направлению каждого из них.
Задача этой лекции – дать первичные знания о законах движения, которые пригодятся как адвокатам по ДТП, так и экспертам, которые подчас «устанавливают» механизм движения путем «размахивания руками» или катания игрушечной машинки по столу.
Целями данной лекции являются:
· дать понятия, что такое производная и интеграл;
· что такое дифференциальное уравнение и как его интегрировать численно;
· решить простейшую практическую задачу – рассчитать движение заторможенного автомобиля.
Производная и интеграл
В конце 17 века в Европе были две крупные математические школы – Лейбница и Ньютона. И обе эти школы пришли к созданию дифференциального и интегрального исчисления, мощного инструмента, без которого наука далее бы не развивалась.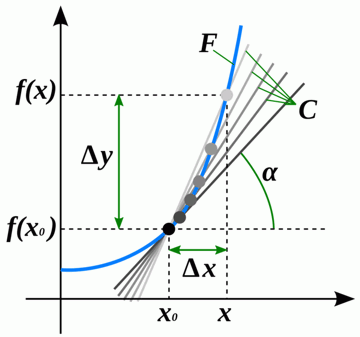
Пусть есть некоторая величина f, которая зависит от x по некоторому закону, который задан некоторой формулой. Тогда говорят, что имеется функция f(x). Для некоторого значения аргумента x=x0 значение функции есть f(x0). Возьмем значение аргумента x, большее чем x0 на малую величину дельта x (греческие символы в тексте не выводятся, поэтому пишу по-русски). Тогда в соседней точке x значение функции будет другое – f(x), отличающееся от величины f(x0) на дельта y. Частное от деления дельта y на дельта x будет тангенсом угла хорды, проведенной на графике функции, как на рисунке выше.
Уменьшая в пределе величину дельта x, получим, что хорда превратилась в касательную к графику функции в точке x, имеющую угол a к оси x. Производной и называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, и записывается это в таких вариантах
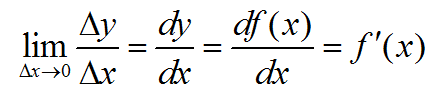 То есть латинская буква d заменяет греческую «дельта», когда величины после этой буквы очень малы, и обозначает дифференциал. Для упрощения производную можно обозначать штрихом, вторую производную (производную от производной) – двумя штрихами и т.д. (на самом деле это римские цифры).
То есть латинская буква d заменяет греческую «дельта», когда величины после этой буквы очень малы, и обозначает дифференциал. Для упрощения производную можно обозначать штрихом, вторую производную (производную от производной) – двумя штрихами и т.д. (на самом деле это римские цифры). Если аргументом функции является время, то производная вместо штриха может обозначаться точкой сверху. Например
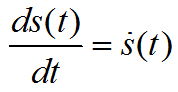 Таблицы производных от основных функций можно посмотреть в Интернете.
Таблицы производных от основных функций можно посмотреть в Интернете.Интегрирование – процесс, обратный дифференцированию, когда надо найти первообразную функцию, производная которой известна. Например
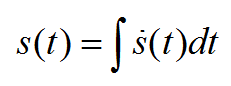 Таблицы интегралов так же есть в Интернете.
Таблицы интегралов так же есть в Интернете.Для целей этой лекции интерес представляют уравнения, связывающие время, путь, скорость и ускорение автомобиля. Если известна зависимость пути s от времени t, или функция s(t), то первая производная от нее по времени есть зависимость скорости от времени v(t), а вторая (или первая производная от скорости) – зависимость ускорения от времени a(t)
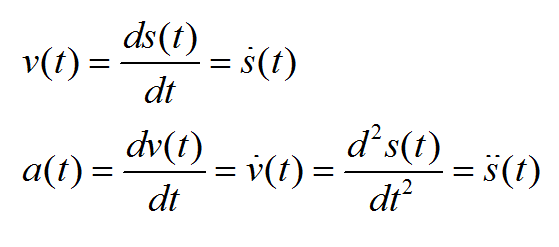 И наоборот, если известна зависимость ускорения от времени a(t), то зависимость скорости от времени v(t) есть интеграл от этой функции, а зависимость пути от времени s(t) есть двойной интеграл от функции ускорения a(t), или интеграл от функции скорости v(t)
И наоборот, если известна зависимость ускорения от времени a(t), то зависимость скорости от времени v(t) есть интеграл от этой функции, а зависимость пути от времени s(t) есть двойной интеграл от функции ускорения a(t), или интеграл от функции скорости v(t) 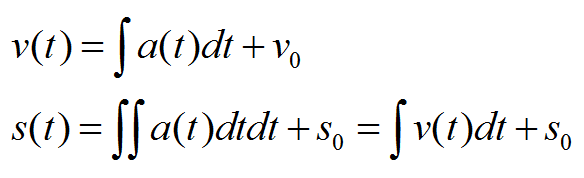 В формуле выше появились постоянные интегрирования – начальная скорость v0 и начальный путь s0.
В формуле выше появились постоянные интегрирования – начальная скорость v0 и начальный путь s0.Юристам, очевидно, пока не понятно, как этими формулами конкретно пользоваться, но сейчас это развеется. Следует отметить, что даже первой группы формул выше достаточно для производства расчетов движения при наличии компьютера, головы и простой вычислительной программы.
Дифференциальное уравнение движения и как его интегрировать численно
В современных терминах 2-й закон Ньютона записывается так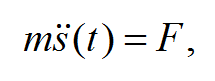 где s(t) – зависимость пути от времени, а две точки сверху есть ни что иное, как ускорение, m – это, конечно, масса, а F – это внешняя сила.
где s(t) – зависимость пути от времени, а две точки сверху есть ни что иное, как ускорение, m – это, конечно, масса, а F – это внешняя сила. Запишем эту формулу в виде, где ускорение есть первая производная от скорости v(t), или, собственно, в формулировке Ньютона
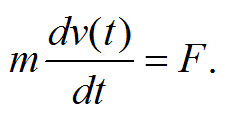 А теперь выделим дифференциал скорости
А теперь выделим дифференциал скорости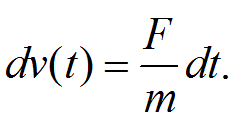 Пусть сила F – сила, действующая на автомобиль при торможении. Тогда она равна произведению массы автомобиля m на ускорение силы тяжести g и на коэффициент сцепления шин с дорогой f, или F=mgf. Тогда масса m в числителе и знаменателе сократится, а произведение gf=j называют замедлением. Замедление – это отрицательное ускорение. Тогда 2-й закон Ньютона принимает вид
Пусть сила F – сила, действующая на автомобиль при торможении. Тогда она равна произведению массы автомобиля m на ускорение силы тяжести g и на коэффициент сцепления шин с дорогой f, или F=mgf. Тогда масса m в числителе и знаменателе сократится, а произведение gf=j называют замедлением. Замедление – это отрицательное ускорение. Тогда 2-й закон Ньютона принимает вид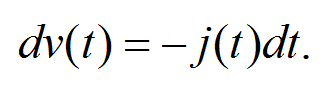 Прочитаем то, что получилось, по-русски: в каждый момент времени дифференциал, или малое изменение (при торможении – уменьшение) скорости есть произведение значения замедления в этот момент времени на дифференциал, или малый интервал, времени. Или, проще
Прочитаем то, что получилось, по-русски: в каждый момент времени дифференциал, или малое изменение (при торможении – уменьшение) скорости есть произведение значения замедления в этот момент времени на дифференциал, или малый интервал, времени. Или, проще Пусть в некоторый момент времени автомобиль имеет скорость v0. Тогда зная значения замедления в этот момент времени и задав малое приращение времени можно просто вычислить значение уменьшения скорости. Вычитая это уменьшение из значения v0, получаем новое значение начальной скорости и повторяем все сначала, пока скорость не станет равной нулю.
Спрашивается, каким же малым должно быть значение приращения времени, 0.01с, 0.001с, …? Это – не вопрос. Компьютеру это по силам, и об этом — ниже.
А путь автомобиля? Путь можно посчитать путем суммирования произведений скорости в каждый момент времени на приращение времени.
Расчет движения заторможенного автомобиля
Рассмотрим, например, движение заторможенного автомобиля по сухому асфальту с момента срабатывания тормозной системы до момента остановки. После блокировки колес замедление автомобиля j нарастает по линейному закону от нуля до установившегося значения 6.8 м/с2 за время нарастания замедления 0.35 с, и далее составляет те же 6.8 м/с2 вплоть до полной остановки. Это можно описать билинейной функцией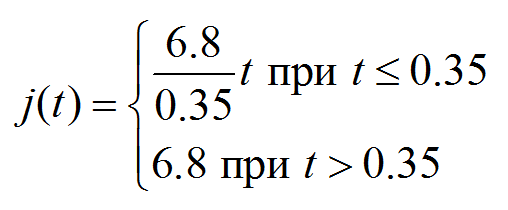 Берем программу Mathcad, на ее листе опишем эту функцию и выведем ее график для контроля.
Берем программу Mathcad, на ее листе опишем эту функцию и выведем ее график для контроля.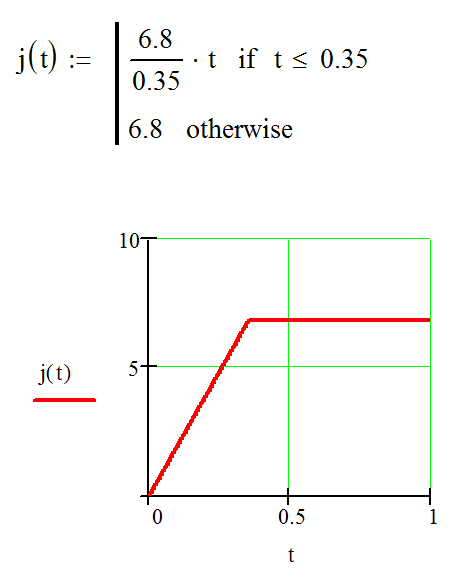 Как видно из рисунка выше пока все правильно.
Как видно из рисунка выше пока все правильно.Зададим начальные данные: интервала времени расчета дельта-t как 0.001 с, начальная скорость автомобиля v0=40 км/ч, начальный путь s0=0 м, начальное значение времени t0=0 с, время расчета движения автомобиля T=2 с.
Тогда скорость и путь автомобиля компьютеру придется считать для N значений времени, где N=2/0.001=2000.
Пусть некий параметр i пробегает значения от 1 до 2000. Для каждого значения i посчитаем значения времени, скорости и пути как
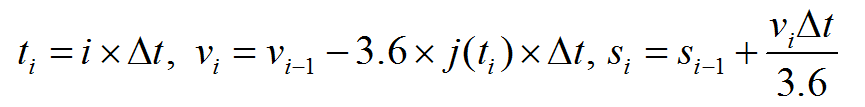 Вот как это записать на листе Mathcad
Вот как это записать на листе Mathcad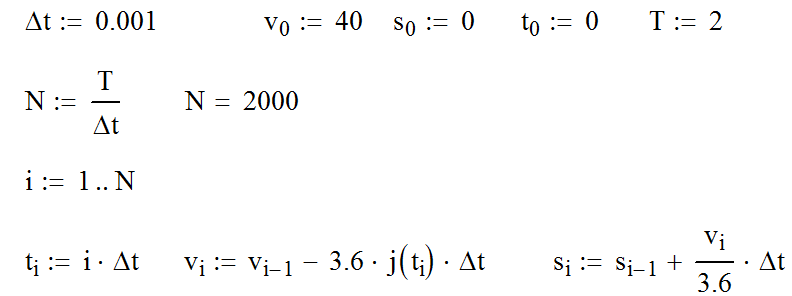
И это – все! Решение получено. Оно содержится в трех таблицах, в первой – в каждой строке время, во второй – скорость в это время, в третьей – путь в это время.
Найдем во второй таблице строку, где скорость автомобиля близка к нулю. Это строка № 1808. Время в первой таблице, соответствующее этому номеру строки, равно 1.808 с, путь в третьей таблице – 10.976 м.
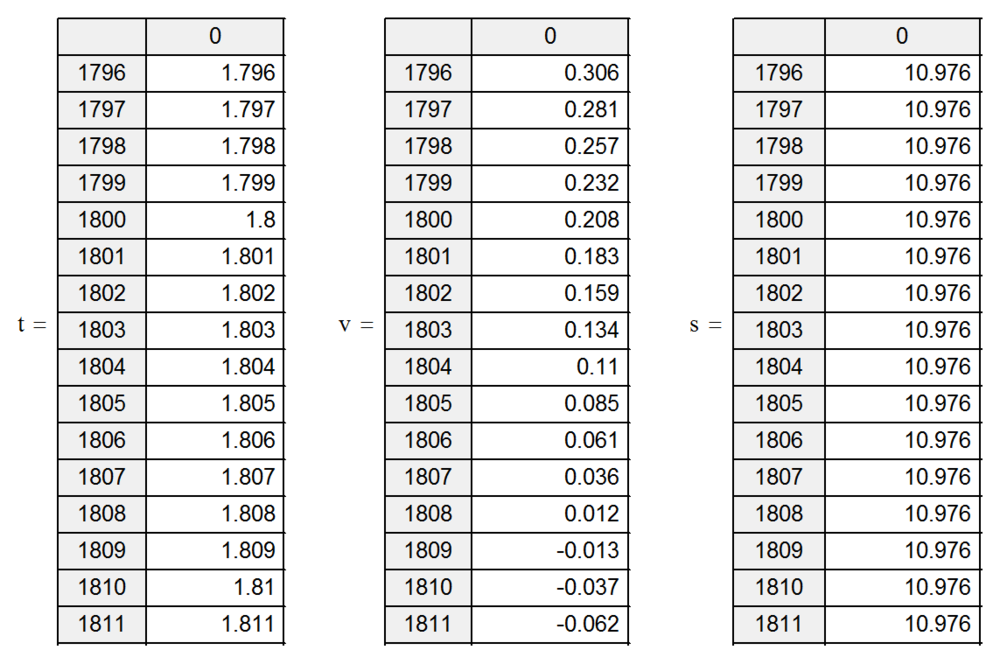
Несколько время 1.808 с и путь 10.976 м точны? Это можно проверить уменьшением интервала времени расчета дельта-t, например принять значение 0.0001 с, или в 10 раз меньше. Современный пентиум выдержит, а мы сравним время и путь при скорости автомобиля близкой к нулю. Точно в ноль попасть сложно, так как это – численный метод, а не аналитический.
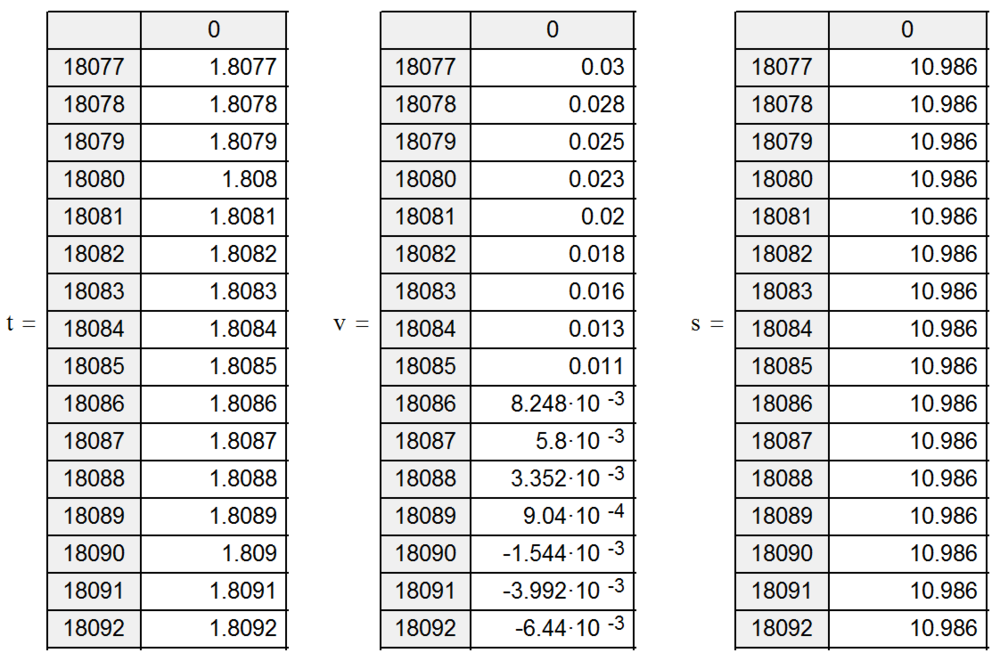
В строке №18089 второй таблицы видим значение скорости 0.000904 км/ч, или, практически, ноль. В соответствующих строках первой и третьей таблиц видим время 1.8089, путь 10.986. То есть, из сравнения с предыдущим результатом, погрешность последнего расчета по времени составляет около 0.001 с, по пути – около 0.01 м. Если считаем что это много, снова уменьшаем интервал времени расчета дельта-t – уже до 0.00001 и повторяем расчет.
Новые значения в строках №180867 времени остановки – 1.80857 с, пути – 10.987 м. Или, из сравнения с предыдущим результатом, погрешность по времени составляет около 0.00033 с, по пути – около 0.001м, или 1 мм.
В заключении эксперта вполне достаточно написать, что расчетное время торможения составляет 1.81с, расчетный путь в заторможенном состоянии – 10.99м.
Надо ли печатать три таблицы с 20-200 тысячами строк в заключении эксперта или приложении к нему? Наверное, нет, если не потребуют особо. Согласно ст.25 ФЗ №73 от 31 мая 2001 г. «О государственной судебно-экспертной деятельности в Российской Федерации», материалы, иллюстрирующие заключение эксперта или комиссии экспертов, прилагаются к заключению и служат его составной частью. Документы, фиксирующие ход, условия и результаты исследований, хранятся в государственном судебно-экспертном учреждении. По требованию органа или лица, назначивших судебную экспертизу, указанные документы предоставляются для приобщения к делу.
Поэтому в заключении эксперта лучше представить расчетные данные визуально, как график зависимости скорости от времени
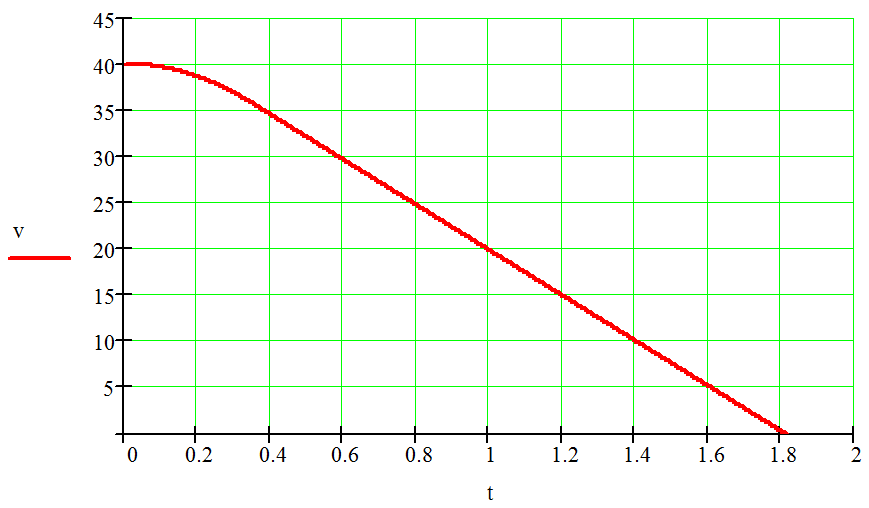 график зависимости пути от времени
график зависимости пути от времени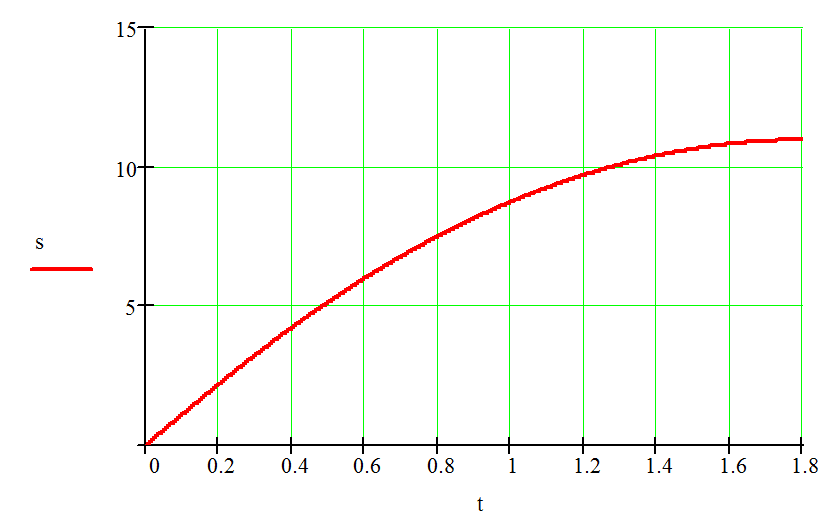 и график зависимости скорости от пути
и график зависимости скорости от пути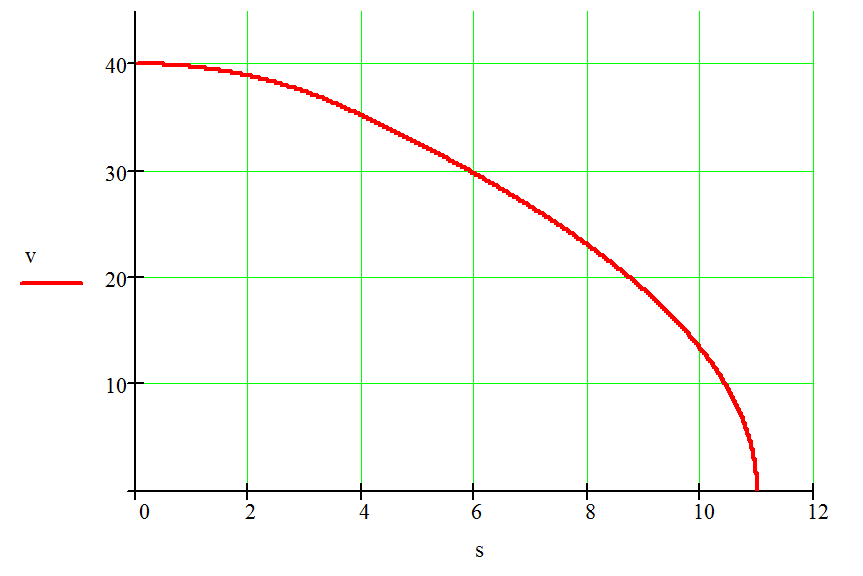
Вполне может сложиться ситуация, когда суд запросит таблицы или их части. Например, если автоэксперт насчитает, имел или не имел водитель техническую возможность остановиться, играя на 2-3 последних сантиметрах тормозного пути.
Проверка результатов
Из методики автотехнической экспертизы путь автомобиля в заторможенном состоянии составляет (26 заменено на точное значение 2х3.62)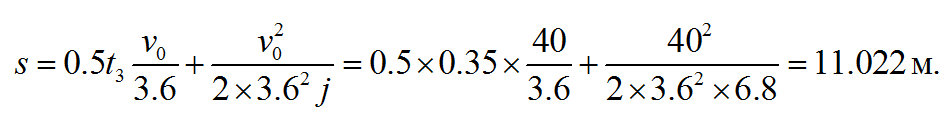
Разность в 0.035 м, или в 3.5 см, между 11.022 м по формуле традиционной автоэкспертизы и 10.987 м численным расчетом с точностью до 1 мм – большая, и вызывает сомнения в точности либо численного расчета, либо традиционных формул. Кто прав, Ньютон или «основоположники от Минюста»?
Прав Ньютон. Дело в том, что отцы-основатели автоэкспертизы при выводе формул остановочного или иного пути автомобиля, где участвует время нарастания замедления t3, выкинули некоторые члены из формул ввиду их малости и дабы у экспертов голова не болела. Строгий вывод формулы приведен в приложении к этой статье, и точное значение пути автомобиля действительно
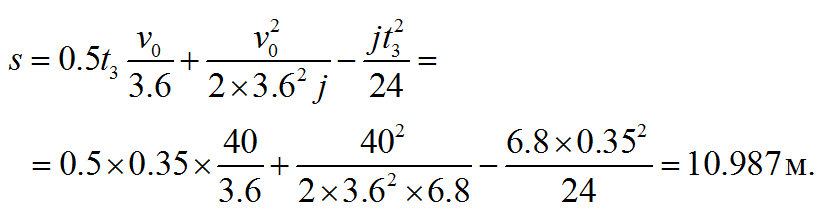 Таким образом, численные методы точнее традиционных методик.
Таким образом, численные методы точнее традиционных методик.Итоги
Итак, адвокаты и юристы, специализирующиеся на ДТП, из этой лекции получили представление о том, как работают специальные компьютерные программы, моделирующие движение автомобилей и их столкновения. В самом деле, кто мешает вместо графика зависимости скорости от времени красиво нарисовать или анимировать положение автомобиля во время торможения?Юристы, адвокаты и эксперты убедились, что численное решение дифференциального уравнения второго порядка на самом деле достаточно простая процедура, которую, однако, проблемно провести без компьютера. В то время как для аналитического решения надо иметь, как минимум, высшее техническое образование, которого нет даже у многих автоэкспертов.
В дальнейших лекциях будет показано, как аналогично можно смоделировать движение автомобиля с вращением, заторможенного или не заторможенного. А цель этих лекций, научить проверять экспертизы, выполненные с помощью специальных программ, оправдывает легкий экскурс в высшую математику.
Юристы и адвокаты, специализирующиеся на ДТП, ранее узнали, что в традиционной методике автоэкспертизы есть грехи. Из этой лекции они узнали, что ошибки вследствие упрощения так же свойственны методикам, ориентированным на ручной счет.
В целом же, эти лекции направлены на создание на «Праворубе» сервиса, позволяющего решать многие задачи реконструкции ДТП в интерактивном режиме.
Литература:
1. Ньютон И. Математические начала натуральной философии. Пер. с латинского А.Н.Крылова. – М.: Издательство АН СССР, 1936.
2. Цывильский В. Л. Теоретическая механика: Учеб. для втузов. – М.: Высш. шк., 2001.
3. Суворов Ю.Б. Судебная дорожно-транспортная экспертиза. – М.: Экзамен, 2003.
Следующая лекция "Уравнения движения. Момент инерции автомобиля"
Все статьи автора на Праворубе.


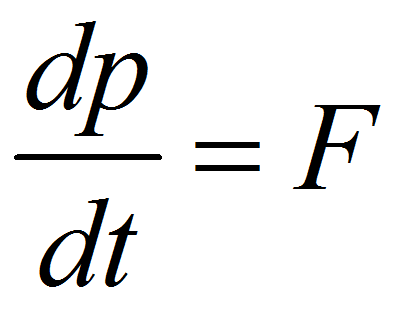


Уважаемый Владимир Николаевич, увидел статью с опозданием в ночь. Ставлю сразу плюс, ознакомлюсь чуть позже. Знаю, что это необходимо и полезно. В какой ещё стране можно за бесплатно получать такие знания! (bow)