И на солнце бывают пятна

«И въ солнцѣ и въ лунѣ есть темныя мѣста!» написал когда-то в поэме «Россияда» Михаил Херасков (1733-1807). И он был прав. По меньшей мере, одно пятно есть и в методике традиционной автотехнической экспертизы, и, в частности, в книге отца отечественной автоэкспертизы проф. В.А.Иларионова «Экспертиза дорожно-транспортных происшествий», М.: Транспорт, 1989.

Про эту ошибку, наверное, не стоило бы писать, если бы она не встретилась автору совсем недавно в заключении одного маститого эксперта. Поэтому адвокатам стоит взять это на заметку.

Речь пойдет об определении скорости заторможенного и вращающегося автомобиля после столкновения – в момента разделения, или о его остаточной скорости. Так как автомобиль вращался и его разные точки прошли после удара разный путь, то речь пойдет о скорости центра тяжести этого автомобиля.

Формула В.А.Иларионова

В.А.Иларионов (на стр. 205 указанной книги) указывает, что эту скорость можно найти, предположив, что кинетическая энергия автомобиля после удара перешла в работу трения шин по дороге во время поступательного перемещения на расстояние S и поворота вокруг центра тяжести на угол e. Работа трения шин на дороге при поступательном движении автомобиля, как известно из школьного курса физики, есть произведение его массы, ускорения силы тяжести, пути центра тяжести и коэффициента сцепления шин с дорогой (фрагмент книги – в приложении).

То же при повороте относительно центра тяжести, где за путь принимается длина дуги окружности, описанной колесами каждой оси при вращении относительно центра тяжести автомобиля.

Приравнивая сумму работы сил трения колес при поступательном перемещении автомобиля и работы сил трения при вращении автомобиля относительно его центра тяжести к кинетической энергии mv²/2, В.А.Иларионов получил значение скорости v в виде формулы 7.20 на стр.205. Единица измерения скорости – м/с.

Для облегчения понимания эта формула упрощена для случая, когда расстояния от осей автомобиля до центра тяжести равны, или a=b и 2a=L. Тогда получается, что

На первый взгляд все правильно, но … В самом деле, положим, что перемещение центра тяжести автомобиля S=0. Он просто крутился на месте в результате удара. Но из формулы вытекает, что v>0. Не странно ли?

А фокус в том, что В.А.Иларионов, имея два вида кинетической энергии, кинетическую энергию поступательного и вращательного движения, каждая из которых была погашена работой сил трения колес в процессах перемещения и вращения, просто их смешал.

Точно так же он мог бы приравнять суммарную работу сил трения при перемещении и вращении автомобиля к кинетической энергии вращения Iw²/2, где I – момент инерции автомобиля (всегда больше, чем масса), w –скорость вращения в радианах в секунду. Тогда он получил бы аналогичную формулу, где слева была бы скорость вращения, а справа – квадратный корень и под ним сумма пути перемещения и угла вращения. И если вращения не было бы, e=0, то есть, автомобиль просто перемещался бы, то все равно из формулы вытекало бы, что w>0. Вот так.

Покажем, что формула В.А.Иларионова дает явно завышенный результат. Для этого проведем и проанализируем численный эксперимент, а затем математический анализ длины пути колес автомобиля при его поступательном и вращательном движении.

Численный эксперимент

В программе Virtual Crash зададим заторможенному автомобилю движение боком вправо с начальной скоростью 30 км/ч. Расстояние между осями виртуального автомобиля составляет 2.54 м, или для формулы В.А.Иларионова a=1.27 м. Коэффициент сцепления шин с дорогой ф=0.7, ускорение силы тяжести g=9.8 м/с².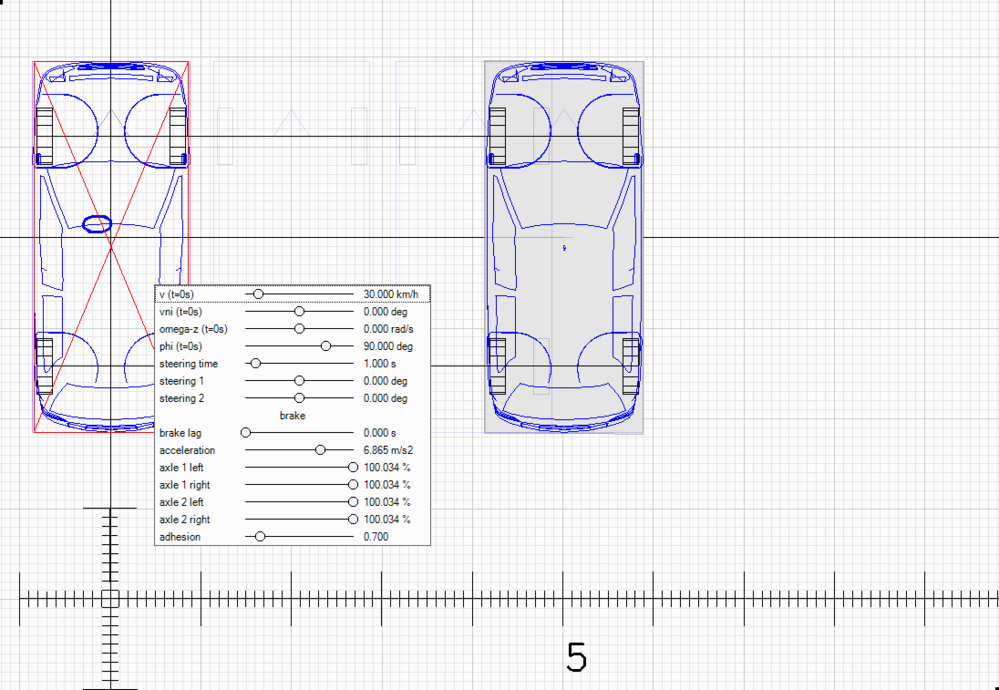


Как видно из рисунка, автомобиль идеально сместился в конечное положение на расстояние S=5.06м. Вращения нет, и формула В.А.Иларионова при e=0 даст правильное решение v=8.33 м/с=30км/ч.

При той же начальной скорости центра тяжести 30 км/ч зададим еще и начальную скорость вращения w=2.18 с^-1, чтобы автомобиль развернулся на угол 90 градусов. Перемещение его центра тяжести составит уже S=5.3м. При этих данных формула В.А.Иларионова дает начальную скорость автомобиля уже v=10 м/с=36 км/ч.


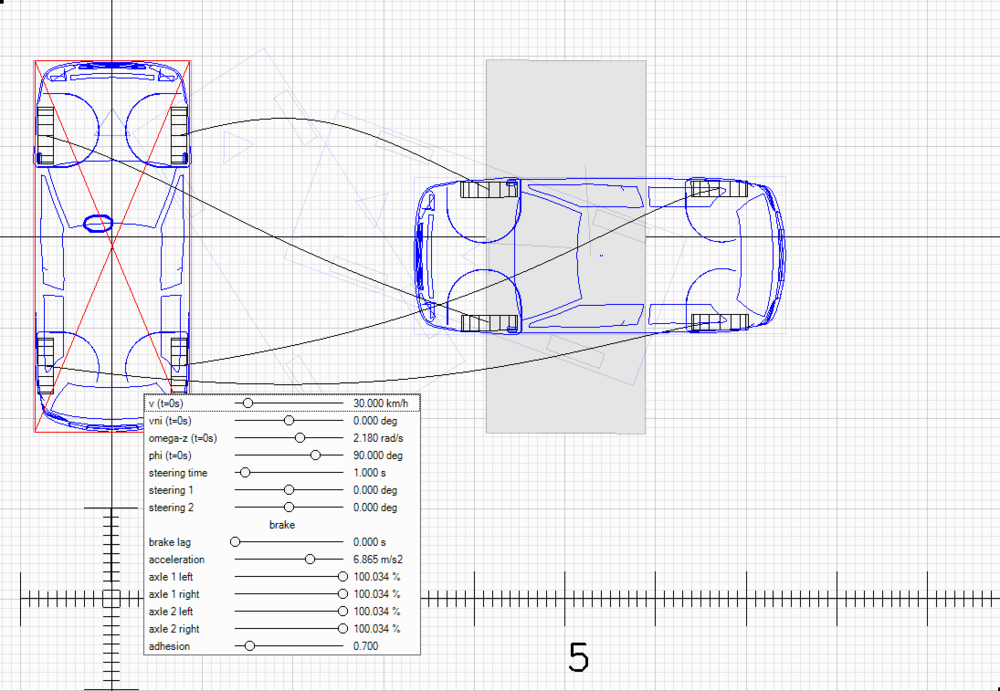
При той же начальной скорости центра тяжести 30 км/ч зададим начальную скорость вращения 8.02 с^-1, чтобы автомобиль развернулся на полный оборот. Перемещение его центра тяжести составит уже S=8.67м. При этих данных формула В.А.Иларионова дает начальную скорость автомобиля аж v=15.1 м/с=54.4 км/ч.


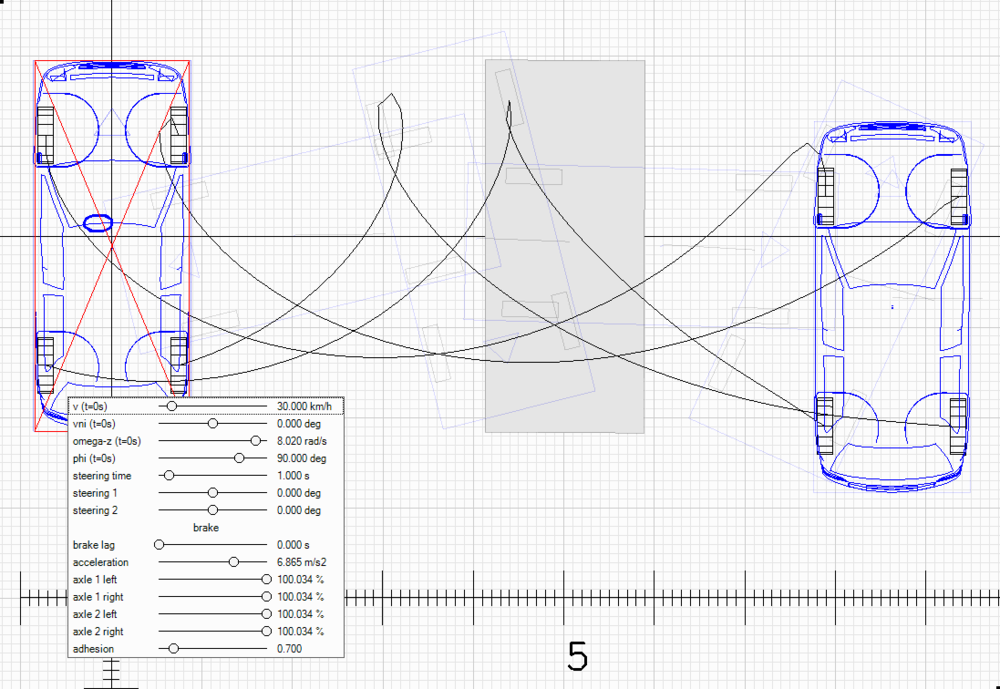
Нравится? Еще бы … Жаль, нет статистики, сколько людей посадили на этой формуле. И пора вскрыть причину, почему эта формула завышает скорость.

Математический анализ длины пути колес

Для адвокатов, «не любящих» математику, ответ на вопрос – сразу. Дело в том, что путь колес автомобиля при его перемещении на одинаковое расстояние и развороте на некоторый угол действительно больше за счет того, что траектории колес становятся криволинейными. Но суммировать длину пути поступательного вращения и длину пути колес при вращении вокруг центра тяжести нельзя, так как часть длины пути вращения уже входит в путь перемещения.

Рассмотрим, для простоты, движение автомобиля, у которого половина расстояния между осями a, с постоянной скоростью движения v и постоянной скоростью вращения w.

Тогда координаты некоторого колеса автомобиля в момент времени t есть

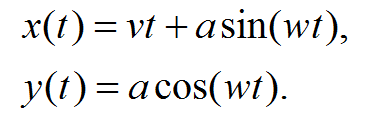Тогда для небольшой скорости вращения траектория этого колеса примерно такая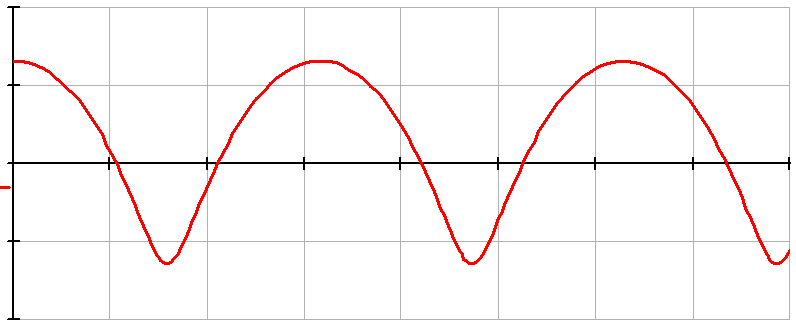


А при большой скорости вращения на траектории появляются петли


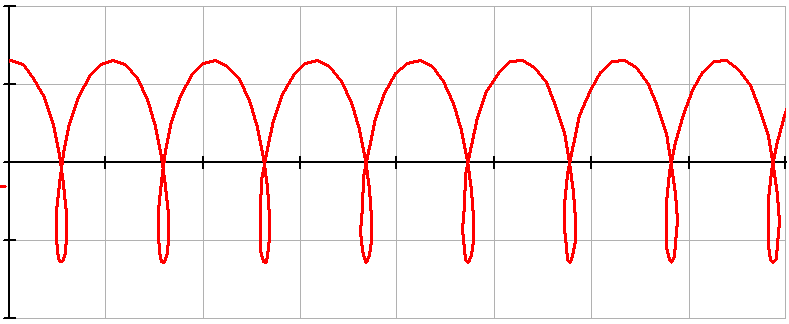
Вычислим длину кривой траектории колеса как

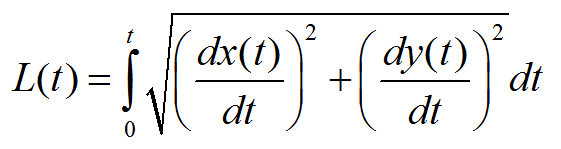и сравним ее с длиной в скобках в формуле В.А.Иларионова выше. Сравнение на графике зависимости длины пути колеса от пути центра тяжести автомобиля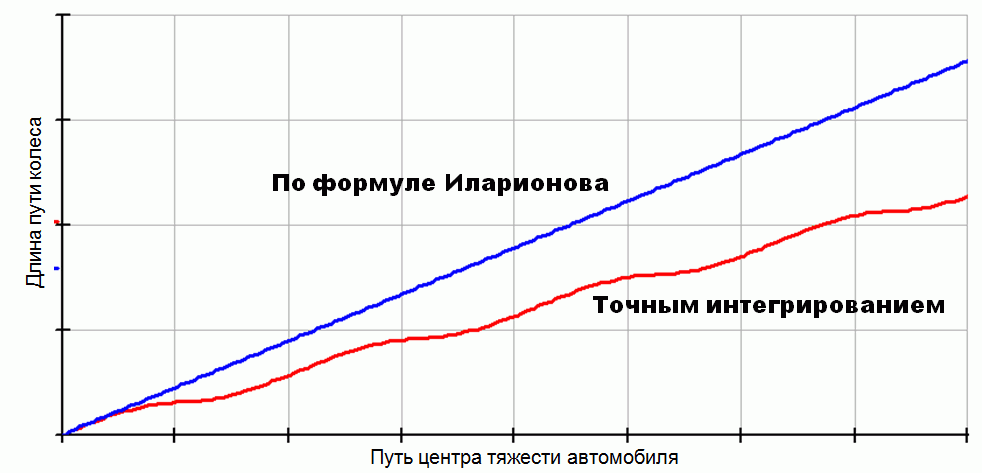


Как видим, путь колеса по формуле В.А.Иларионова всегда больше фактического пути колеса, полученного точным интегрированием. При увеличении угла разворота автомобиля разница между кривыми становится больше.

Резюме

Таким образом, доказано, что формула из методики автотехнической экспертизы, предназначенная для установления скорости автомобиля с учетом его угла разворота в результате удара, ошибочная и дает завышенные значения.

И на солнце бывают пятна.

Все статьи автора на Праворубе