Установление места столкновения автомобилей для случая разворота автомобиля вблизи места столкновения

Опубликованная ранее в журнале «Уголовный процесс» и на сайте «Праворуб» методика установления места столкновения расчетным путем содержит общий алгоритм, включающий две части. Как следует из практики, эксперты достаточно неплохо усваивают первую, более простую, часть этой методики, но затрудняются реализовать вторую часть, как правило, из-за слабых навыков программирования. В этой статье показано, как в ряде часто встречающихся на практике особых случаев столкновения, заменить более сложную вторую часть методики простым дополнением ее первой части. Кроме экспертов, эта статья будет полезна следователям и адвокатам в части знания возможностей современных экспертных методик.

Первая часть методики содержит метод установления затрат кинетической энергии автомобилей на деформацию в каждой точке дороги, как в возможном месте столкновения. Из установленных затрат энергии на деформацию автомобилей и их масс получают величины изменения скорости автомобилей в результате удара. Тогда зная конечное положение центров тяжести автомобилей для каждой точки дороги можно установить и их скорости в момент столкновения как сумму остаточной скорости и изменения скорости с учетом их знаков, а, значит, и установить затраты кинетической энергии на деформацию. Из сравнения полученного поля этой энергии с фактическими затратами энергии на деформацию определяется место столкновения.

Вторая часть методики содержит алгоритм уточнения, если полученная в первой части область достаточно велика, или велики затраты энергии на вращение автомобилей в результате эксцентричного удара.

Однако в ряде часто встречающихся случаев энергию вращения можно исключить сразу, при использовании несколько измененного алгоритма первой части.

Теория

Пусть на некоторый неподвижный объект массой m и с моментом инерции J=k²m (k – радиус инерции объекта) относительно вертикальной оси, проходящей через его центр тяжести С, действует импульс S.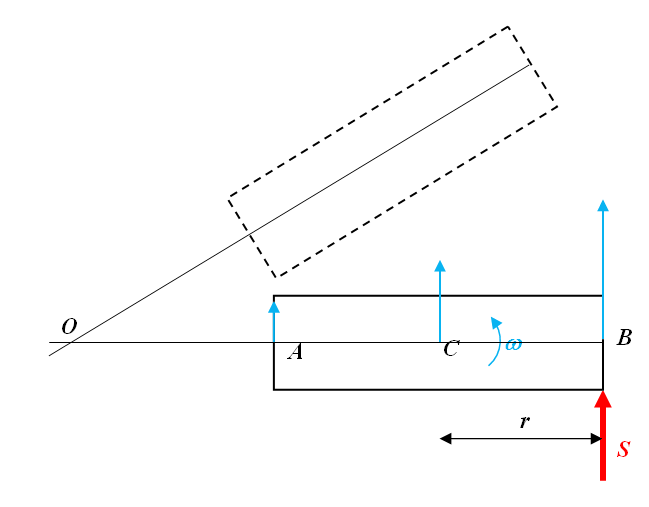

В результате объект получает скорость центра тяжести и скорость вращения
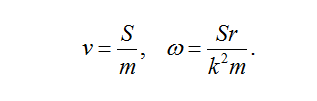Тогда кинетическая энергия объекта есть сумма энергий поступательного и вращательного движений
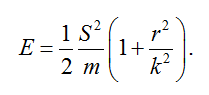Второй член в скобках, отношение квадрата плеча импульса к квадрату радиуса инерции, может быть близок к единице, когда плечо импульса сопоставимо с радиусом инерции. Или остаточная кинетическая энергия объекта практически удваивается за счет эксцентричности удара.

Согласно теореме Гюйгенса-Штейнера момент инерции объекта относительно произвольной неподвижной оси равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр тяжести объекта, и произведения массы тела на квадрат расстояния между этими осями.

Рассматривая начальное и конечное положение объекта, на самом объекте или вне его всегда можно найти точку, как точка О на рисунке, перемещение которой в результате удара было наименьшим, а движение объекта можно представить как сумму перемещения этой точки и вращения объекта вокруг нее. Суммарная кинетическая энергия объекта при этом не изменится – это инвариант, не зависящий от способа расчета. Однако использование такой точки вместо центра тяжести, как фиктивный центр тяжести, позволит исключить из выражения для кинетической энергии вращательную часть. При этом, как следует из теоремы Гюйгенса-Штайнера, исключается возможная наибольшая величина количества вращательного движения.

Пример

Рассмотрим столкновение двух заторможенных одинаковых автомобилей массой 1324 кг, с моментом инерции 1750 кг*м², смоделированное в программе Virtual Crash. Левый на рисунке (синий) в момент столкновения имел скорость 18.8 км/ч, после удара — 22.4 км/ч. Правый (зеленый) в момент столкновения имел скорость 68.8 км/ч, после удара — 32.9 км/ч. Или, в результате удара синий автомобиль изменил свою скорость на обратную на 18.8+22.4=41.2 км/ч, зеленый уменьшил скорость на 68.8-32.9=35.9 км/ч.



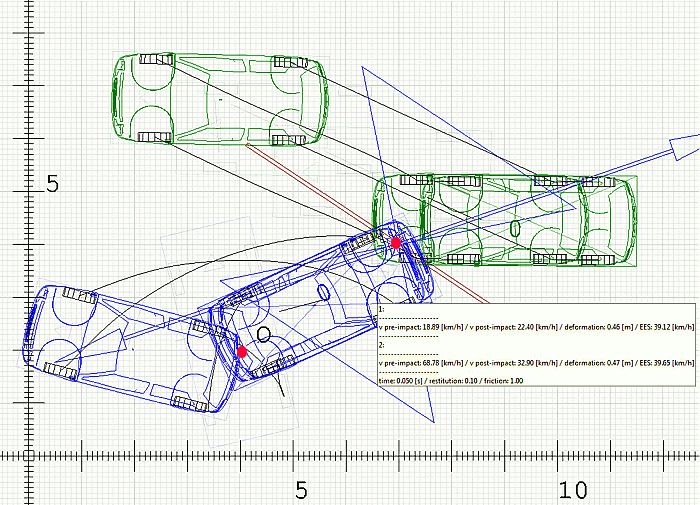
Зеленый автомобиль в результате практически центрального удара существенно не развернуло. Поэтому для него будем рассматривать положения его центра тяжести в момент удара +2.4м по оси Х, и +0.4 м по оси Y относительно точки столкновения.

Синий автомобиль, как видно из рисунка, существенно развернулся в результате эксцентричного удара. Развернулся вокруг некоторой точки контура задней части, находящейся между положениями задней части его правого заднего колеса в момент удара и в конечном положении. Далее принимаем эту точку за фиктивное положение его центра тяжести, чем избегаем сложных расчетов по второй части методики. Положение этой точки относительно точки столкновения в момент удара было -2.8м по оси Х и -2.1м по оси Y.

Далее проверяем область дороги с шагом 0.1м. Листинг программы для MathCad приведен в приложении к статье.




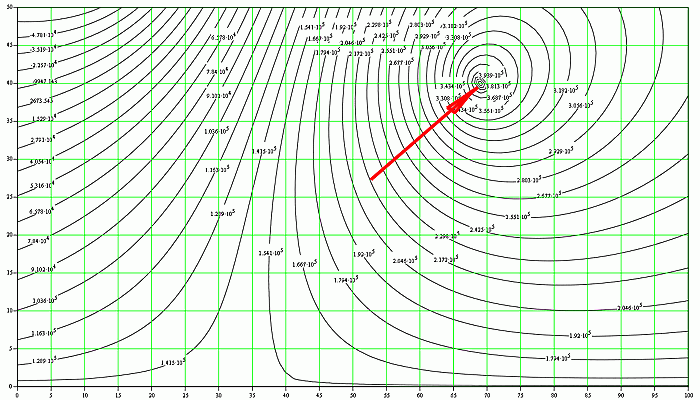
Как видно из полученного поля затрат энергии на деформацию, без учета вращательного движения, в данном случае сильно исказившего бы результат, место столкновения находится в точке с координатами 6.8м по оси Х и 4.0м по оси Y.  Что мы и видели выше на рисунке со схемой столкновения.

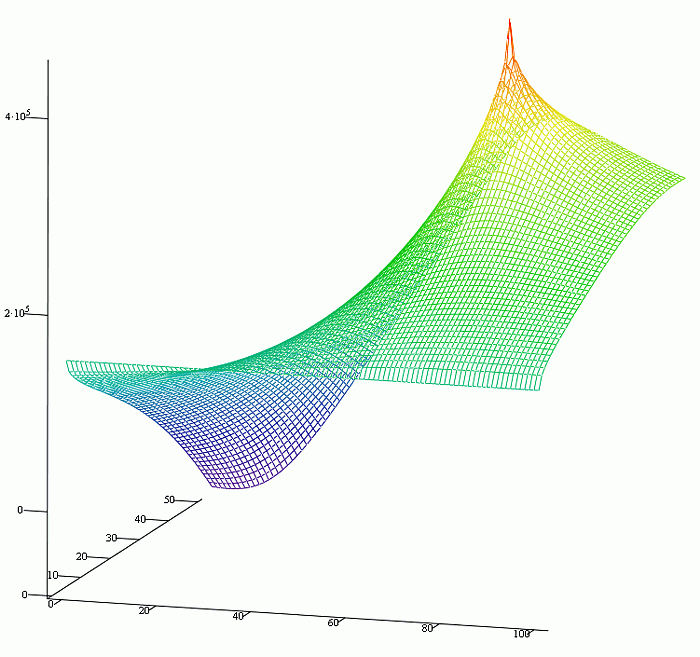
Из рассмотрения поля затрат энергии на деформацию в трехмерном виде видно, что расчетная область места столкновения мала, и дальнейших уточняющих расчетов не требуется.





Резюме

Теоретическая механика разработана в общем виде. И сейчас, и в будущем, вместе с научно-техническим прогрессом, возникают и будут возникать задачи, которых нет в учебниках, но способы их решения давно есть. Это – одна из таких задач. Экспертам ее надо усвоить, а адвокатам – взять на заметку. Если же эксперты в суде будут читать молитвы типа «нами не проверено, не апробировано, науке неизвестно …», не верьте таки шаманам, даже если поверят прокурор и судья. Придет время, и все встанет по своим местам.