Еще раз про расчет места столкновения. Для экспертов, следователей и судей

Есть в судебной экспертизе методическое пособие, под заголовком которого в скобках написано «для экспертов, следователей и судей». И не случайно – там нет сложных формул, а изложены политые кровью на дорогах истины. В том числе то, что место столкновения не определяется по положению крупных осколков автомобилей, таких, например как фара или багажник, если нет следов их движения. Эти части могли попасть в свое конечное положение, как отделившись в момент удара, так и потом, при вращении автомобиля, и разлететься веером куда угодно, могли изменять свою траекторию движения и … Одному богу, короче, известно, как и что. Но обвинить в нашей стране человека по положению двух таких осколков вполне возможно путем «колхозного голосования».

Так, на южном берегу одного из наших северных морей госэксперт не установил место столкновения по положению фары и багажника. Адвокат одного из участников обращается в Уфу для расчета места столкновения, а второй участник едет не куда-нибудь, а в столицу, где независимые эксперты ему пишут, что «очень может быть, что столкновение произошло на Вашей полосе, уважаемый …» и даже, почесав себе репу, из нее же рисуют схемы движения автомобилей «согласно физике». Уже теплее. Находят другую контору, куда уже следователь назначает экспертизу, и там, со ссылкой на первых гадальщиков, эксперты, один из которых оценщик, продолжают эти же фантазии.

Колхозное голосование? Да! И еще, по принципу «Пастернака не читал, но скажу» пишут нечто абсурдное про мою методику расчета места столкновения, даже формулы пишут, что-то туда подставляют и вычисляют, может и правильно, но не понимая совершенно, что и зачем.

Методику расчета места столкновения публиковал на Праворубе адвокат А.Куприянов, публиковал и я, но решил вернуться к этому вопросу еще раз, на простейшем примере – для экспертов, следователей и судей. На что надеюсь? По меньшей мере, на порядочность и мужество наших первых фантазеров – признают, что накуролесили, или будут стоять, как столпы правосудия?

Поэтому, сегодня – пример, а фактическое дело с фамилиями, паролями и явками – потом. На «Праворубе», Бастрыкину, Лебедеву … Пора. Смотреть концерт молча я не собираюсь.

Итак, рассмотрим удар двух одинаковых деформируемых материальных точек массой 1 кг каждая. Их размеры столь малы, что место соударения совпадает с положением их центров масс. Точка №1 движется со скоростью v1=(7,0), или проекция ее скорости на ось X равна 7 м/с, а на ось Y – нулю. Точка №2 движется со скоростью v2=(-5,3). В начале системы координат XY они сталкиваются. Точки движутся с трением о поверхность, пусть замедление равно f=5 м/с².

В результате удара между ними возникает действие и противодействие, или на первую точку действует импульс s=(-3, 3.842), и, соответственно, на вторую точку – противоположный импульс -s=(3, -3.842).

Очень важное замечание. Закон сохранения количества движения – рамочный закон, в его записи неизвестных больше, чем уравнений. Импульс можно приложить любой, но фактически реализуется процесс, в котором среди множества возможных импульс действует такой, который обеспечивает минимальные затраты энергии на деформацию объектов. Я этот импульс определил, а как – суть сейчас не в том.

Величина затрат энергии на деформацию составила 23.765 Дж. В результате удара точка №1 уменьшает свою скорость на 1.454 м/с и оказывается в конечном положении с координатами (2.219, 2.131), точка №2 – на 3.661 м/с и оказывается в (-0.434, -0.183). Это и является исходными данными для обратной задачи – по конечному положению, величине затрат энергии на деформацию и соответствующим ей изменениям скоростей, с учетом известных масс точек и замедления при движении, установить место их столкновения.

Рассмотрим область, в разумных пределах, от х=-1 до х=3 и от y=-1 до y=3, или размером 4х4 метра. В каждой точке (x,y) области с шагом 0.1 м определим Z1 – расстояние от этой точки плоскости до конечного положения материальной точки №1, и Z2 – расстояние от этой точки плоскости до конечного положения материальной точки №2.

Далее вычислим остаточные скорости материальных точек №1 и №2, как если бы столкновение произошло в этой точке плоскости (x,y), чтобы они могли попасть в свои конечные положения, или U1 и U2 соответственно.

Прибавляя к полученным значениям остаточных скоростей материальных точек U1 и U2 в рассматриваемой точке плоскости (x,y) значения изменения скоростей материальных точек, получаем величины их скоростей V1 и V2 в момент столкновения, если бы это столкновение имело место в точке (x,y) области.

Как финальный аккорд, в рассматриваемой точке плоскости (x,y) вычислим значение A – разность кинетической энергии обоих материальных точек до и после удара, или затраты энергии на их деформацию.

Результат выведем в виде изолиний и трехмерной поверхности, которую пересекает плоскость равного уровня энергии деформации 23.765 Дж.

На рисунке ниже – лист маткада с вычислениями.


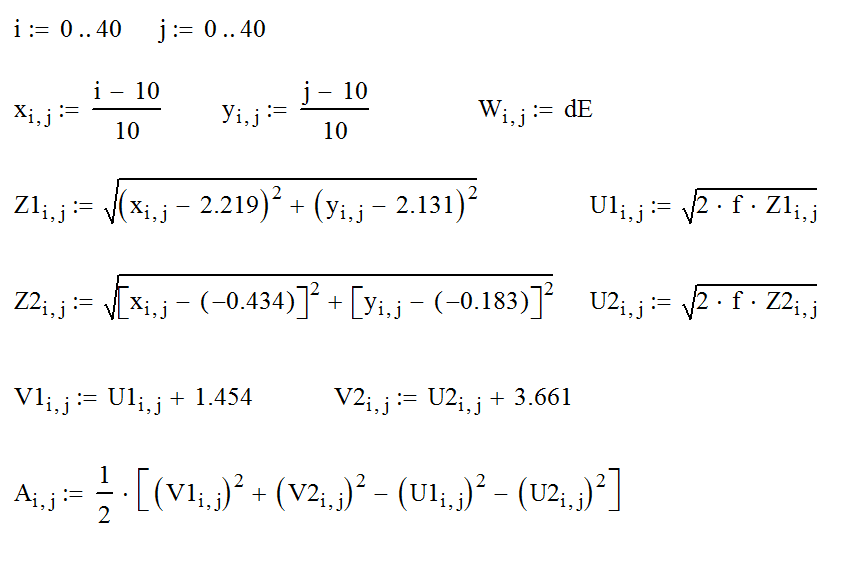На рисунке ниже – изолинии равных затрат энергии.


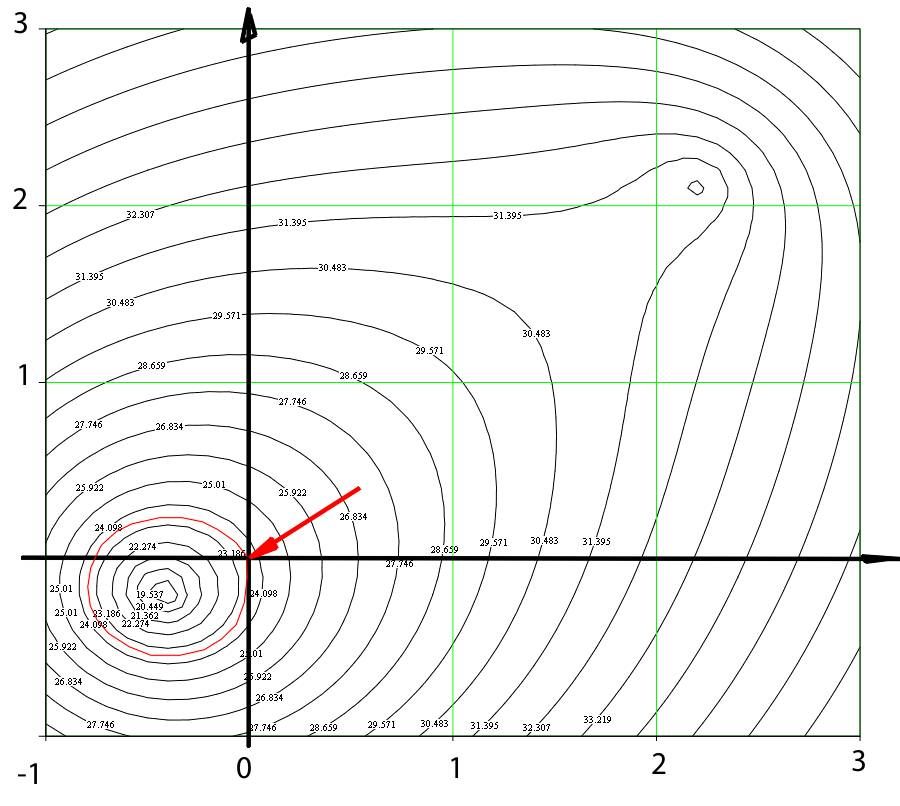На рисунке ниже – трехмерная поверхность затрат энергии и плоскость уровня 23.765 Дж. Начало координат здесь смещено в точку (-1, -1), по осям абсцисс и ординат размеры в дециметрах. То есть реальная точка столкновения — это  (10,10).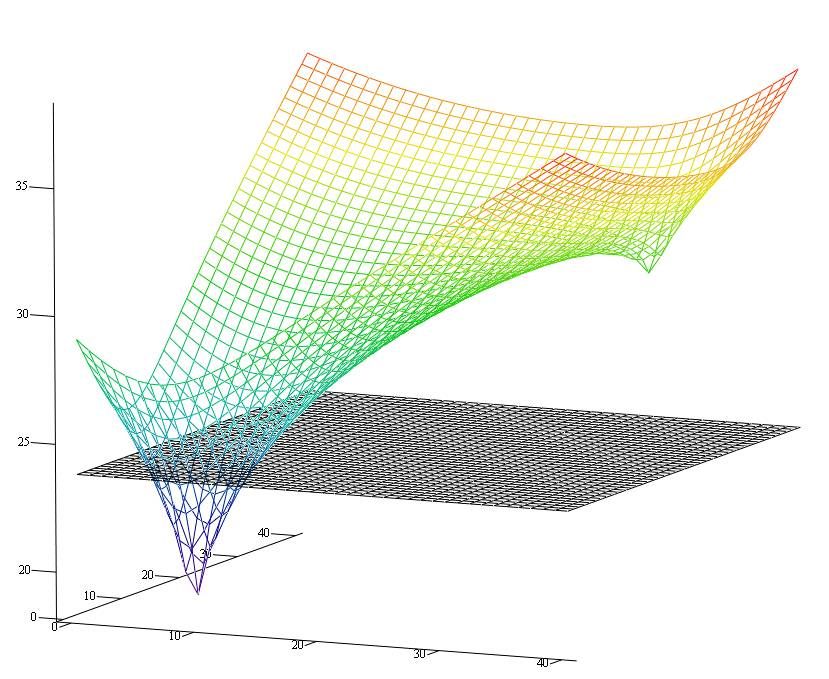



Как видно из результатов на графике изолиний, столкновение материальных точек могло произойти на выделенной красным цветом изолинии 23.765 Дж, в том числе в начале координат. Чтобы уточнить решение, на этой изолинии надо проверить выполнение законов сохранения импульса и момента импульса. Но для реальных автомобилей подобная область часто получается столь мала, что ее размеры не требуют дальнейших расчетов.

А экспертам хочу сказать, что если и это неясно, то бросьте заниматься ДТП. Одно дело громко говорить про законы физики, другое – их применять. В конце концов, народ должен знать своих героев поименно. А я помогу.